Variable Control Chart Formulas and Calculations
This pages summarizes the calculations used for the control charts including plotted values, process sigma, process average and control limits. The calculations are divided up as follows:
- Subgroup Charts (X-R, X-s, X, R, s, Median-R, Median)
- Individuals Charts (X-mR, X, mR, z-mR, Levey_Jennings, Run)
- Between/Within Charts (X-mR-R, X-mR-s)
- Between/Within Charts (X-mR-R, X-mR-s)
- Multivariate Charts (T2)
Subgroup Charts (X-R, X-s, X, R, s, Median-R, Median)
Plotted Values
Subgroup Average: the average of the values in the subgroup; the equation below shows the average for the ith subgroup containing ni values; plotted on the X chart.
Note: the software handles varying subgroup sizes.
Subgroup Range: the range of the values in a subgroup; the equation below shows the range of the ith subgroup where Xmax is the maximum value in the subgroup and Xmin is the minimum value in the subgroup; plotted on the range (R) chart.
Ri = Xmax – Xmin
Subgroup Standard Deviation: the standard deviation of the values in a subgroup; the equation below shows the standard deviation of the ith subgroup where Xij is the jth sample in subgroup i, Xi is the subgroup average, and ni is the number of values in the subgroup; plotted on the s (standard deviation) chart.
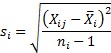
Subgroup Median: the median of the values in a subgroup (the “middle” value if the subgroup size is odd; the average of the two middle values if the subgroup size is even); plotted on the median chart.
Process Sigma
Sigma: sigma (s) can be estimated from the average subgroup range, from the average subgroup standard deviation, or from the pooled standard deviation.
Sigma from Average Range (default option on all subgroups charts except X-s control chart): the following equation is used to estimate sigma:
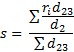
where
and ri is the range for the subgroup i, d2 and d3 are control chart constants that depend on subgroup size (ni).
Sigma from Average Subgroup Standard Deviation (default for X-s control chart): the following equation is used to estimate sigma:
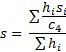
where
and where si is the standard deviation of the ith subgroup and c4 is a control chart constant that depends on subgroup size (ni).
Sigma from Pooled Standard Deviation: the following equation is used to estimate sigma:
s = sp/c4
where
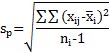
and where sp is the pooled standard deviation, c4 is a control chart constant that depends on subgroup size, xij is the jth sample of the ith subgroup, xi is the average of the ith subgroup and ni is the subgroup size for the ith subgroup.
Process Averages
Overall Average: The overall average is the average of all the individual sample results. This will equal the average of the subgroup averages if the subgroup size does not vary. However, if the subgroup size varies, the average of the subgroup averages does not equal the average of the individual sample results. The software uses the individual sample results to calculate the overall average.
Average Range: the average range for a subgroup depends on the subgroup size using the following equation:
R = d2s
where d2 is the control chart constant based on the subgroup size (ni) and s is the estimate of the sigma.
Overall Average Median (Xm): the overall average median is the average of the subgroup medians.
Control Limits
X Chart Control Limits
where X is the overall average, nsl is the number of sigma limits (default is 3), n is the subgroup size, and s is the estimate of sigma.
R Chart Control Limits
where nsl is the number of sigma limits (default is 3), d2 and d3 are the control chart constants based on the subgroup size (n), and s is the estimate of sigma.
s Chart Control Limits: the upper control limit (UCLi) and the lower control limit (LCLi) for subgroup i are given by the following equations:
where nsl is the number of sigma limits (default is 3), c4 and c5 are the control chart constants based on the subgroup size (ni), and s is the estimate of sigma.
Median Chart Control Limits: the upper control limit (UCLi) and the lower control limit (LCLi) for subgroup i are given by the following equations:
where Xm is the average subgroup median, nsl is the number of sigma limits (default is 3), e1 is a control chart constant to adjust sigma for using the median instead of the average for the subgroup size (n), and s is the estimate of sigma.
Individual Charts (X-mR, X, mR, z-mR, Levey-Jennings, Run)
Plotted Values
X Values: the individual values; plotted on the X chart, Levey-Jennings chart, and run chart.
z Values: the z values for a given product; the following equation is the ith z value for product j, Xi the ith value for product j, ?j is the estimated sigma for the product (based on the moving range of 2), Nominalj is the nominal value for product j (can also use the average of product j); plotted on the z chart.
zi = (Xi-Nominalj)/?j
mR Values: the moving range between consecutive points, the following equation is the ith moving range, Xi and Xi-1 are two consecutive points; plotted on the moving range (mR) chart.
Ri – |Xi – Xi-1|
Process Sigma
Sigma: sigma (s) is estimated from the moving range for the X-mR, X, mR, and z-mR chart; the Levey-Jennings uses the calculated standard deviation; the run chart does not require an estimate of sigma.
Sigma from the Average Moving Range: the following equation is used to determine sigma, where mR is the average moving range and d2 is a control chart constant that depends on subgroup size (SPC for Excel uses n = 2 for the moving range).
Sigma from the Calculated Standard Deviation: the following equation is used to determine sigma for the Levey-Jennings chart, where Xi is the ith value, X is the overall average and N is the total number of values.
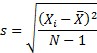
Process Averages
The overall process average for individuals charts is calculated from the individual samples except for the z-mR chart.
Overall Average: the average of the individual samples, except for z chart: process average is always 0.
Average Moving Range: the average moving range is given by:
mR = d2s
where d2 is the control chart constant based for n = 2 and s is the estimate of sigma from the average moving range.
Process Averages
X Chart Control Limits
where nsl is the number of sigma limits (default is 3), and s is the estimate of the sigma from the average moving range.
mR Chart Control Limits
where nsl = number of sigma limits, s = estimate of sigma from the average moving range, and d2 and d3 are control chart constants set for a subgroup size of 2.
z Chart Control Limits
UCL = 3
LCL = -3
Levey-Jennings Chart Control Limits
where nsl is the number of sigma limits (default is 3), and s is the estimate of the sigma from the calculated standard deviation.
Between/Within Charts (X-mR-R, X-mR-s)
The calculations for these charts are the same as those given above for the X, R, s, and mR charts. Please refer to those calculations.
Time Weighted Charts (MA/MR, EWMA, CUSUM)
Note: the moving average/moving range (MA/MR) chart calculations are the same as given for the subgroup averages charts above. Please refer to those calculations.
CUSUM Chart: One-Sided
Plotted Values
One-Sided Upper CUSUM: the one-sided cumulative sum on the “high” side (above the average).
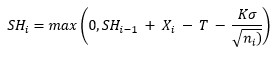
where SHi = upper CUSUM for ith sample, SHi-1 = upper CUSUM of (i-1)th sample, Xi = ith sample result, T = target, K = difference to detect, ? = estimated standard deviation, ni = size of ith sample (note: X represents an individual sample results or a subgroup average).
One-Sided Lower CUSUM: the one-sided cumulative sum on the “low” side (below the average).
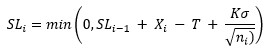
Note: if the fast initial response option is not selected, SH0 = SL0 = 0. If the fast initial response option is selected (F = value of fast initial response) then:
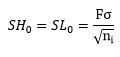
Process Average: the average for the CUSUM is 0.
Process Sigma:
If the subgroup size is 1, sigma is estimated from the moving range for n = 2 (see above); if the subgroup size is greater than 1, sigma is estimated as the pooled variance (see above).
Control Limits
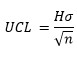
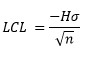
where H = action limits.
CUSUM Chart: V-Mask
Plotted Values
Cumulative Sum Statistic: the cumulative sum of the difference from target.
Si = Si-1 + Xi – T
where S0 = 0, Xi = the ith sample, and T = target.
Process Average: the average for the CUSUM is 0.
Process Sigma
If the subgroup size is 1, sigma is estimated from the moving range for n = 2 (see above); if the subgroup size is greater than 1, sigma is estimated as the pooled variance (see above).
Control Limits
For the last point (H = action limits):
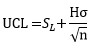
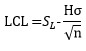
For remaining points (K = difference to detect):
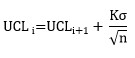
EWMA Chart
Plotted Values: the exponentially weighted moving average determined by:
EWMAi = EWMAi-1 + w(Xi – EWMAi-1)
where w = the weighting factor, Xi = ith sample result (or subgroup average).
Process Sigma: if the subgroup size is 1, sigma is estimated from the moving range for n = 2 (see above); if the subgroup size is greater than 1, sigma is estimated as the pooled variance (see above).
Process Average: this is the target value or the overall average.
Control Limits
where nsl is number of sigma limits (default is 3), s = estimate of sigma, CL is the center line (either the average or the target), w = weight, and n= subgroup size.
Multivariate Charts (T2)
Plotted Values
Subgroups
where n = subgroup size, x = subgroup average, x = overall average, S = S matrix
Individuals
where x = individual sample, x = overall average and S = S matrix.
Control Limits
Subgroups
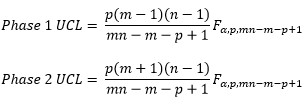
where n = subgroup size, m = number of subgroups, p = number of variables, ? = confidence level, F is the F distribution.
Individuals
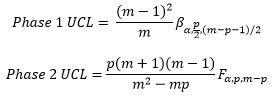
where B is the beta distribution.