Two Sample Equivalence Test Help
This test is used to determine if there is a practical difference between two averages. One average is considered the reference average. The other average is considered the test average. The difference being examined is the test average minus the reference average. The user must determine how much of a difference in the averages is significant. You use your knowledge of the process to determine this. This test can be two-sided or one-sided.
The example below demonstrates how to do this test. You can download the data at this link.
A company produces a cleaning liquid. One component is a key. A new product has the same component. The company wants that component level to be the same in both. The current cleaning liquid is the “reference” data. The new one is the “test” data. The company is will for the test product to vary from -1 to 1 from the reference cleaning liquid. Samples for each product are taken and tested for the component. The steps to perform the analysis with the SPC for Excel software are given below.
1. Enter the data into a worksheet as shown below. The data must be in columns. One column represents the test data; the other column, the reference data. The software assumes that the first column is the test data, but it does not have to be.
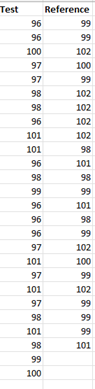
2. Select the data above (including the heading).
3. Select “Equivalency Tests” from the “Statistical Tools” panel in the SPC for Excel ribbon.
4. Select the “Two Sample Equivalency Test.” The input form below is shown.
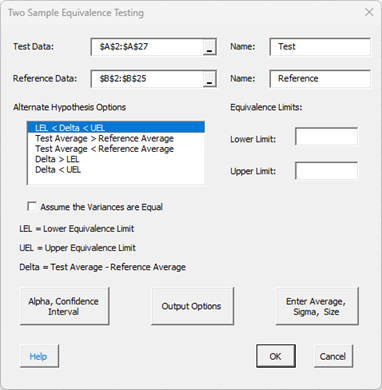
- Test Data: This is the worksheet range containing the test data; the default is the selected worksheet range.
- Name: The name of the test data if it is present in the first cell above the test data.
- Reference Data: This is the worksheet range containing the reference data; the default is the selected worksheet range.
- Name: The name of the reference data if it is present in the first cell above the reference data.
- Select the Alternate Hypothesis (H1 ) Option; the first option is the default and is a two-sided test; the rest are one-sided tests.
- LEL < Delta < UEL
- Test Average > Reference Average
- Test Average < Reference Average
- Delta > LEL
- Delta < UEL
where Delta = Test Average – Reference Average, LEL = lower equivalence limit and UEL = upper equivalence limit.
- Lower Limit: Enter the lower equivalence limit; the LEL in this example is -1.
- Upper Limit: Enter the upper equivalence limit; the UEL in this example is 1.
- Assume the Variances are Equal: The calculations can include the assumption that the variances are equal or that they are not equal; the default is to assume that the variance is not equal.
- Alpha, Confidence Interval: The input form below is shown if this option is selected.
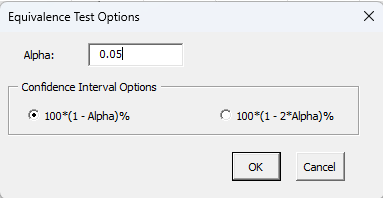
- Alpha: This is the confidence level; 1-alpha is the confidence interval; default is 0.05 or 95% confidence interval.
- Confidence Interval Options: Select the option you want to calculate the confidence interval; this option is only available if the Lower Equivalence Limit < Average – Target < Upper Equivalence Limit option is selected for H1 .
- Select OK or Cancel to return to the first input form above.
- Output Options: the input form below is displayed if this option is selected.
- First Cell of Output Range on this Worksheet: Select this option if you want the output on an existing worksheet; then select the first cell of the range where you want the output placed; a check is made to ensure that no existing data are overwritten in the worksheet.
- New Worksheet: Select this option if you want the results on a new worksheet.
- Enter Average, Sigma and Size: the input form below is displayed if this option is selected.
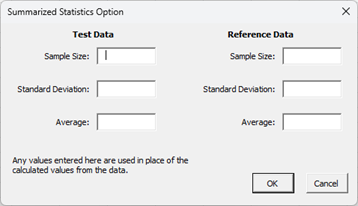
- You may enter the sample size, standard deviation, or the average for the test and reference data; any value that is entered will be used in place of the values calculated from the data.
- Select OK or Cancel to return to first input form above.
- Select OK to generate the results.
- Select Cancel to end the program.
Two Sample Equivalence Test Output
The output from the example data is shown below. A new worksheet is added to the workbook. The LEL = -1 and the UEL = 1 in this example. The alternate hypothesis chosen was Lower Equivalence Limit < Average – Target < Upper Equivalence Limit.
An explanation of terms is given below the output. In addition to the output table, the program displays charts that help interpret the results.
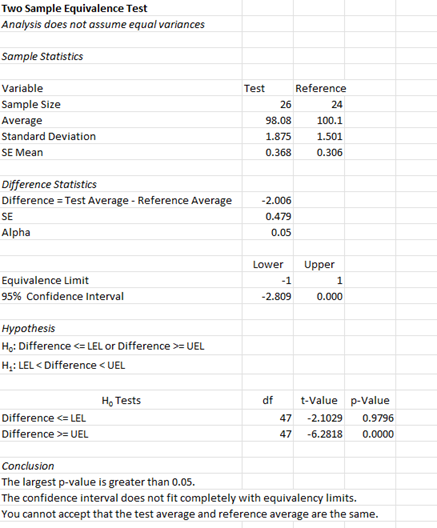
- Sample Statistics for both datasets:
- Variable: Name of variable
- Sample Size: Number of data points
- Average: Calculated average of data
- Standard Deviation (s): Calculated standard deviation
- Standard Error of Mean: Calculated as standard deviation/sqrt(sample size)
- Difference Statistics
- Difference = Test Average – Reference Average
- SE: Standard Error
- Alpha: Value entered by User (default is 0.05)
- Equivalence Information
- Equivalence Limits: Lower and Upper entered by user
- 95% Confidence Interval: Calculated Lower and Upper values
- Hypothesis
- H1 : selected by user.
- H0 : based on H1
- H0 Tests
- H0 Tests: Based on which H1 hypothesis was chosen
- df: Degrees of freedom
- t-Value: Calculated t-Value
- p-Value: Calculated p-Value
- Conclusions
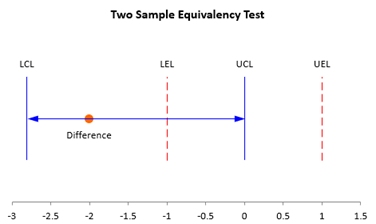
- Gives the conclusion of whether the target and average are the same based on the p-value and the confidence interval and equivalency limits; in this example, one p-value is larger than alpha and the confidence interval does not fit within the equivalency limits, so you cannot assume that the test average and reference average are the same.
The chart below is also created. This makes it easy to see if the confidence interval for the difference is within the equivalence interval.
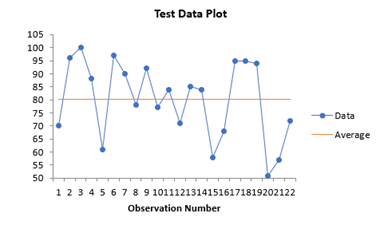
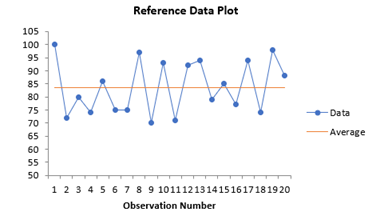
There are also two charts – one for the test data and one for the reference data – to look for possible outliers. If the program detects possible outliers, they will be in red and a message will be printed on the worksheet.