Exponential Growth Time Series Analysis Help
Home » SPC for Excel Help » Analysis Help » Time Series Analysis Help » Exponential Growth Time Series Analysis Help
The Exponential Growth time series analysis is used to analyze data that has a trend and no seasonal component. In addition, the trend has curvature to it, i.e., it is not a linear trend. The Exponential Growth model used for the fit is:
Yt = b0(b1t)
where
- Yt = the value of the data at time t
- b0 = a constant
- b1 = the coefficients for time
This help page describes how to perform the Exponential Growth time series analysis using the SPC for Excel software using data that can be downloaded at this link. This page contains the following:
Data Entry
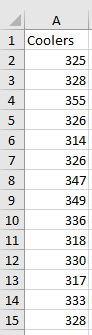
Enter your data in a spreadsheet as shown below. The data must be in a single column with or without a heading. The data can be anywhere in the spreadsheet. There can be no empty cells or non-numeric entries in the data (except if there is a heading). It is important that the data represent evenly spaced data in time.
Running the Analysis
Select the data on the worksheet to be included in the analysis. You just have to put the cursor in the first row (the data or the heading as shown above). The software will select the data automatically then.
To start the analysis, select “Time Series” under the “Analysis” panel on the SPC for Excel ribbon. The form below is shown.
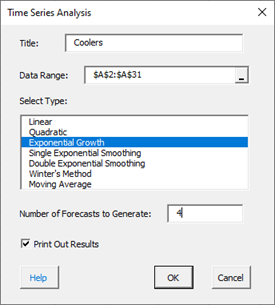
- Title: this is the data name; the default is the first cell in the data column if it is non-numeric; otherwise it is blank.
- Data Range: the range containing the data; if this range is not correct, it can be edited here.
- Select Type: select the time series method you wish to use; Exponential Growth in this example
- Number of Forecasts to Generate: enter the number of forecasts you want; the default is 0.
- Print out Results: this option prints out the results in a spreadsheet including the model, MAPE, MAD, MSD, the actual values, the fitted values, the residuals, and the forecasts if any; the default is to print out the results. This output is in addition to the chart that is created (see below).
- Select Cancel to stop the analysis.
- Select OK to create the analysis.
Output
The output from the Exponential Growth time series analysis consists of two parts: the chart and the printed results (if that option was selected).
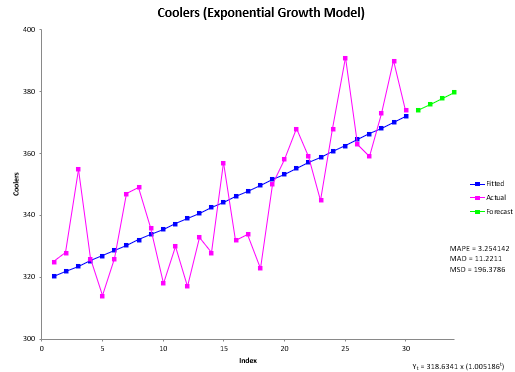
The Exponential Growth chart is shown below. It includes the actual values, the fitted values, the values of MAPE, MAD, and MSD, as well as the best fit equation. Forecasts, if included, are also shown. The best-fit equation is used to calculate the forecasts.
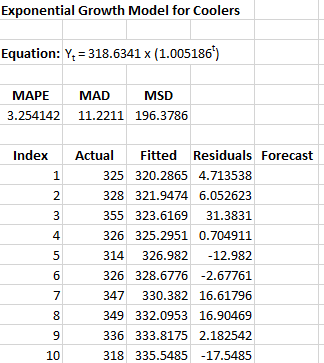
The printed results are shown below. It includes the same information as in the chart but in tabular format.
Interpretation of Output
The first thing to do is to examine the chart of the fitted line with the actual values. Decide if it fits the data. The points should be randomly distributed around the fitted line. If the points do that, then it is probably a good fit. If you ran other models, you compare the three accuracy measures (MAPE, MAD, and MSD) described in the first time series help page. The smaller the values, the better the fit.
If there are forecasts values, you can check to see how good they might be. You want the fitted line to closely follow the actual results. If it begins to vary at the end of the actual data, something may be changing (like the trend).
