z-mR Control Charts for Short Production Runs

July 2015

“We are pretty much a job shop. Our production runs are short. We are always changing over to a different product. Each job is different. We can’t use SPC here.”

Heard that before – or something similar? One of the purposes of statistical process control (SPC) is to ensure that a process remains in statistical control, i.e., ensure it is consistent and predictable. To make a control chart, you take data over time. Once you have enough data, you calculate the average and control limits. The more samples you have, the better your estimates of the average and control limits. Then you plot everything and interpret the control chart. At some point, you set the control limits and use those to judge the future performance of the process.

But how can you do this when you only get one, two or three data points (samples) during a production run? You could set up a control chart for each product and hope that, over time, you get enough data to make a control chart. But, then you would have a lot of control charts to manage.

This month’s publication takes a look at how you can handle this type of situation – how to use control charts with short-runs. In particular, we will take a look at the z-mR control chart. In this issue:

• Introduction to z-mR Control Charts
• Example Data
• Calculation of z Values
• Control Limit Calculations for the z-mR Control Chart
• Plotting the z-mR Control Charts
• Using the z-mR Control Chart Effectively
• Summary
• Quick Links

You can download a pdf copy of this publication at this link. Please feel free to leave a comment at the end of the publication.

Introduction to z-MR Control Chart

Suppose you have a process that makes 10 different parts on a routine basis. Each run is “short” – you might just get a couple samples for each part. You may be able to chart each individual part on its own control chart, but then you would be maintaining 10 different control charts. The z-mR control chart offers you a way to handle this situation. This chart is introduced below.

A z-mR control chart is two charts. One chart is for the z value which is the “standardized” X value. It is determined by the following equation:

z=(X-X)/σ

where X is the sample result,X is the average, and σ is the standard deviation. You will have a different average and standard deviation for each part. Subtracting the average from the sample result and dividing by the standard deviation “standardizes” the results. This calculation creates the z distribution which has an average of 0 and a standard deviation of 1.

The z values are plotted over time. Since the z values are standardized, the average on the z control chart will be 0 and the control limits will be at +3 and -3. These represent +/- 3 standard deviation limits and the standard deviation is equal to 1.

The mR control chart is the moving range chart. It monitors the variation between consecutive z values. The average and control limits for the mR control chart are set also. The average is 1.128 and the upper control limit is 3.686. These are derived below.

The process for creating a z-mR control chart is given below using an example of a process that creates two different products using short production runs.

Example Data

Suppose you make two products but regularly switch back and forth between those two products. Sometimes you might have one sample for a production run, other times two or three. The data for the last 30 samples you have collected are in shown in Table 1.

Table 1: Example Data

So, the first sample came from a Product 1 production run. The second sample came from a Product 2 production run; samples 3 to 6 came from another Product 1 production run; samples 7 – 10 came from another Product 2 production run, etc. We will use these data to construct the z-mR control chart.

Calculation of z Values

The equation for determine the z value of a sample was given above. Calculating a z value for each sample requires an estimate of the average and standard deviation for each product. The data above can be used to calculate the average and standard deviation for the two products.

The average is determined as usual – add up the sample results for a product and divide by the number of samples. The average for each product is given below:

Product 1 Average: 19.5

Product 2 Average: 8.3

The standard deviation (or sigma) is not calculated using the basic equation for the standard deviation. Instead, it is calculated as it should be when using control charts and individual values – from the moving range between consecutive samples. Table 2 shows the results for Product 1. The moving range is determined as the absolute value between consecutive values. So, the first moving range is given by |20-25| = 5. The second moving range is |25 – 17| = 8 and so on.

Table 2: Moving Range Calculation for Product 1

The estimated standard deviation is then determine by dividing the average moving range by 1.128 (the control chart constant for a moving range of 2).

σ = R/1.128

The average moving range for Product 1 is 5.1. So the estimated standard deviation for Product 1 is:

Product 1 Standard Deviation= 5.1/1.128 = 4.5

The standard deviation can for Product 2 can be estimated using the same procedure and it is equal to 2.1.

The z values can now be calculated for the data in Table 1. The first sample in Table 1 was for Product 1 and the sample result was 20. Thus the z value is given by:

z₁ = (X-X₁)/σ₁ = (20-19.5)/4.5 = 0.11

The average and standard deviation for Product 1 was used in the above calculation. What does this value of z mean? It means that the sample result of 20 for Product 1 is 0.11 standard deviations above the average for Product 1.

The second sample in Table 1 was for Product 2 and the sample result was 5. The z value for this sample is found using the average and standard deviation for Product 2:

z₂ = (X-X₂)/σ₂ = (5-8.3)/2.1 = -1.57

This value of z means that the sample result of 5 for Product 2 is 1.57 standard deviations below the average for Product 2. The z values for the other samples in Table 1 can be found using the same approach. Table 3 contains the calculated z values.

Table 3: Example Data with z Values

Control Limit Calculations for the z-mR Control Chart

The control limits for the z control chart are straightforward. The average is always 0 and the control limits are set at -3 and 3. This is because we take each sample result for a product, subtract the average from the result and divide by the standard deviation for the product. This standardization creates a distribution with an average of 0 and a standard deviation of 1. So, for the z control chart:

Average = 0; LCL = -3; UCL = 3

The average moving range and control limits for the mR control chart are also set. The equation to calculate sigma from the average moving range above can be re-arranged to give the following:

σ(R) = 1.128

Since sigma = 1, the average moving range is 1.218.

The upper control limit for the mR control chart is given by the following:

UCL_R = 3.267R = (3.267)(1.128) = 3.686

There is no lower control limit for a mR control chart when n = 2. So, for a mR control chart based on z values, the average moving range is 1.128, the upper control limit is 3.686 and there is no lower control limit.

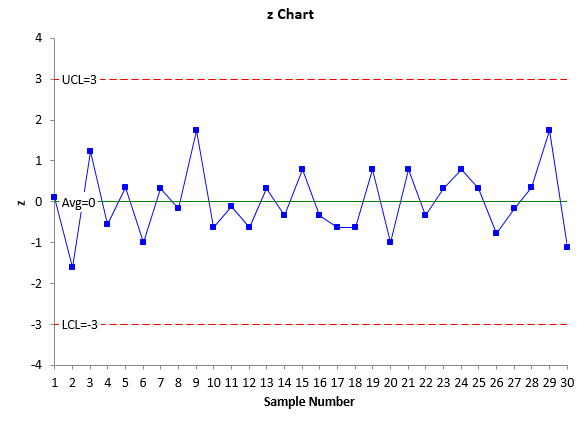
Plotting the z-mR Control Charts

The z values have now been calculated along with the moving range between the z values. The average and control limits have been set. The z-mR control charts can now be created. The z values are plotted on one chart along with the average of 0 and the lower and upper control limits of -3 and 3, respectively.

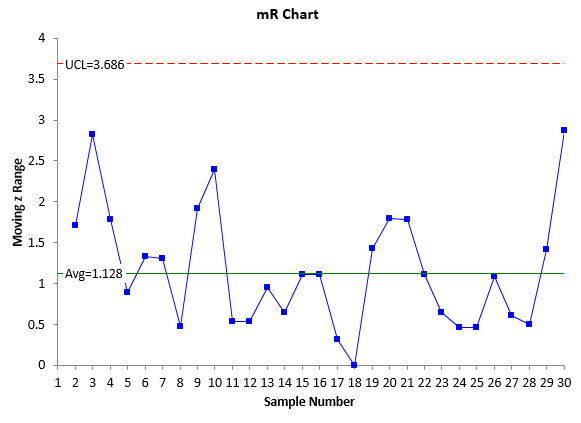
The moving ranges are plotted on another chart along with the average moving range of 1.128 and the upper control limit of 3.686. The z-mR control chart is shown in Figure 1. The top part of Figure 1 is the z control chart. All the basic tests for out of control points apply – points beyond the control limits, the zone tests, etc. There are no out of control situations on this chart. This z control chart is in “statistical control” – it is consistent and predictable. The bottom part of Figure 1 is the moving range chart. This chart is in statistical control as well. The moving range is predictable.

Figure 1: z-mR Control Chart

Using the z-mR Control Chart Effectively

Once you have sufficient data on your products, you “set” the history. This means that you do not change the estimates of the average and standard deviation and use these to track the process over time. The data in Table 1 has 15 samples of Product 1 and 15 samples of Product. The z-mR control chart in Figure 1 is consistent and predictable – in statistical control. So, you decide to set the history based on these samples and not change the averages and standard deviations in the future.

Suppose you do that and continue to monitor the results over time. You have collected additional data. These data are shown in Table 4.

Table 4: Additional Data

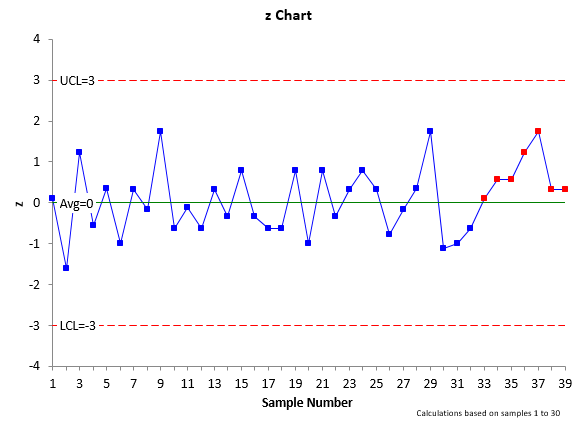
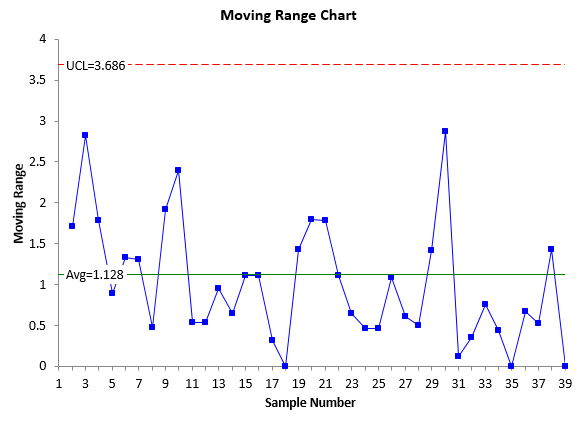
Figure 2 shows the control chart with the additional data. The z control chart is no longer in statistical control. There is a run of 7 above the average line (0). This means that something has happened to cause the z values to increase over these 7 runs. This special cause should be found and eliminated. This is the way that the z-mR control chart can be effectively used to determine when a special cause exists in your process.

Figure 2: z-mR Control Chart with Additional Data

Summary

This publication has shown one method of using SPC with short production runs. The z-mR control chart can be used to handle this type of situation. The methodology involves calculating a z value for each sample using the estimated product average and standard deviation. Doing this allows all the products to be placed on the same control chart. The averages and control limits for both the z chart and the moving range chart are set and do not change.