Equality of Variances (ANOVA)
There are two methods for comparing the equality of variances:
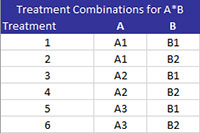
The output below is for the example being used in this section with all the factors being fixed factors and for comparing A*B. When comparing components with more than one factor, the program first generates a table of treatment combinations as shown below. Treatment 1 is A at level A1 and B at level B1. Treatment 2 is A at level A1 and B at level B2. The comparisons are then based on these treatments.
Bartlett’s Test
Bartlett’s Test is used to determine if the treatment variances are the same. The output for this example is shown below for the A*B treatment combination.
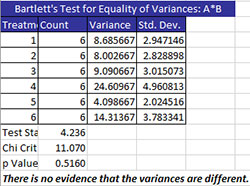
The treatments are listed along with the count, the variance and standard deviation for each treatment. The following three statistics are given:
- Test Stat: this is the value of the chi-square test statistic (where N = total number of observations, a = number of treatments, and Si2 is the variance of the ith treatment.
- Chi Critical: this the critical chi-square value based on alpha and the degrees of freedom (which is the number of treatments – 1); if the test stat > chi critical, reject the null hypothesis
- p value: Reject the null hypothesis if p value < alpha
- The conclusion is given: in this case there is no evidence that the variances are different
Modified Levene’s Test
The Modified Levene Test is used to determine the equality of treatment variances. The output for this example is shown below.
The treatment combination is listed along with the count, the variance and standard deviation. The following three statistics are given:
- F Levene: This is the Levene statistic given by (where N = total number of observations, a = number of treatments, Dij = absolution deviation of the jth observation from treatment i mean, Dbari = average of ni absolute deviations from treatment i, Dbar = average of all N absolute deviations)
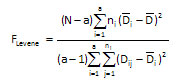
- F Critical: This the critical value of F based on alpha with a-1 degrees of freedom in the numerator and N-t degrees of freedom in the denominator; reject the null hypothesis if F Levene > F Critical.
- p value: reject the null hypothesis if p value < alpha
- The conclusion is given: in this case there is no evidence that the variances are different