October 2004
In this issue:
Process improvement is not bringing a process into statistical control. Bringing a process into statistical control is putting the process where it should be. Once the process is in statistical control, real efforts at process improvement can begin. Process capability is one method of measuring the effectiveness of a process in meeting standards or customer specifications as well as measuring process improvement efforts. This newsletter presents Part 1 of Process Capability.
Process Capability Explanation
Histograms graphically display the variation in a process. Once our process is in control, we know that if we take samples and construct a histogram from yesterday’s, today’s, or tomorrow’s product, the histogram will look basically the same in terms of shape, average, and standard deviation.
For processes that are in statistical control and that are normally distributed, we can do a process capability analysis.
Is your weight “capable” of meeting the guidelines set by insurance companies?
For example, if you are 5’9″ in height and are a male, you should weigh between 139 and 175 pounds, according to Metropolitan Life Insurance Company. Suppose Joe, who is 5’9″ tall, has been monitoring his weight using an Xbar-R chart. Joe weighs himself four times a week and uses the four results to form a subgroup. Joe would like to know if his weight is “capable” of meeting the guidelines. The control chart indicates that Joe’s “weight” process is in control. The average (Xbar) on the chart is Joe’s estimate of the true weight. Suppose that average is equal to 155:
The variation in his individual weighings (standard deviation, s ) is estimated from the average range on the range chart. Suppose that the estimated standard deviation is 2.
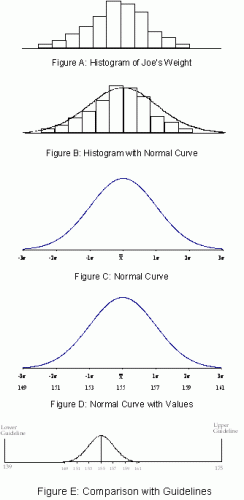
The next step is for Joe to construct a histogram based on the individual results (weighings). Suppose that the histogram Joe constructed looks like Figure A. This histogram appears to be normally distributed (bell shaped). To see this, Joe can superimpose a normal distribution on the histogram (Figure B).
Since the histogram appears to be normally distributed, Joe makes the assumption that his “weight” process can be represented by a normal distribution. Thus, instead of using the actual histogram, Joe will use the curve in Figure C to determine if his weight is capable of meeting the insurance guidelines.
For a normal distribution, the high point on the curve is the average (155). About 68% of the process output lies within +/- 1 s of the average, about 95% lies within +/- 2 s of the average, and about 99.7% lies within +/- 3 s of the average. To determine the values for these different distances from the average, add or subtract the correct number of s from the average:
+1 s from the average: 155 + 2 = 157
-1 s from the average: 155 – 2 = 153
+2 s from the average: 155 + 2(2) = 159
-2 s from the average: 155 – 2(2) = 151
+3 s from the average: 155 + 3(2) = 161
-3 s from the average: 155 – 3(2) = 149
Since Joe has now determined the values to use on the normal distribution, he adds them to the graph as shown in Figure D.
Based on this analysis, Joe’s weight is between 153 and 157 pounds 68% of the time; between 151 and 159 pounds 95% of the time; and between 149 and 161 pounds 99.7% of the time. Since Joe’s “weight” process is in statistical control and can be represented by a normal distribution, Joe can now compare the above distribution to the guidelines set by the insurance company. The upper limit is 175 pounds; the lower limit is 139 pounds. This comparison is shown in Figure E.
Since the distribution fits entirely inside the guidelines, Joe’s “weight” process is capable of meeting the insurance company’s guidelines. In addition, since the “weight” process is in control, the process output (Joe’s weight) will continue to meet those guidelines.
Customers want to know if the products they buy are capable of meeting their specifications, i.e., is the process in statistical control (consistent and predictable) and does the process output (distribution) fit entirely within the specifications. There are two mathematical indices that help customers determine this. These are Cpk and Cp. Cp is covered in this month’s newsletter. Cpk will be covered next month.
Cp Index
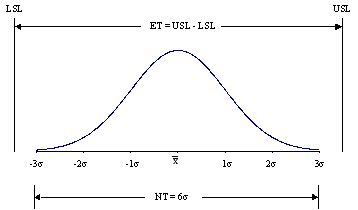
The natural tolerance is the distance from -3s to +3s. If the specifications or standards are outside the distribution, the process is meeting specifications. The upper specification limit (USL) minus the lower specification limit (LSL) is called the engineering tolerance (ET).
One capability ratio, Cp, is defined as the ratio of the engineering tolerance to the natural tolerance:
Cp = ET/NT = (USL – LSL)/(6s)
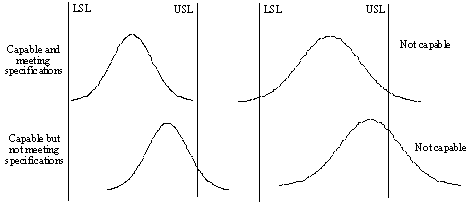
If the engineering tolerance is less than the natural tolerance (i.e., Cp < 1.0), the process is not capable of meeting specifications. If the engineering tolerance is equal to or larger than the natural tolerance (Cp > 1.0), the process is capable of meeting specifications. A process can be capable of meeting specifications but not be meeting specifications if the process is not centered relative to the specifications. Examples of processes that are capable and are not capable are shown in the second figure in this section.
Cp Example
A team in an operating unit has been working on improving yield from a batch reactor. The process is in control and the individual yield readings form a normal distribution. The average yield is 80.2% with a standard deviation of 2.79. Internal specifications for the yield are LSL = 75 and USL = 85. The value of Cp is calculated as follows:
Cp = ET/NT = (USL – LSL)/(6s)
Cp = (85 – 75)/6(2.79) = 0.60
Since the Cp value is less than 1, you know that there are batch yields that are not within the internal specifications. And, since the process is in control, you must fundamentally improve the process to reduce the amount of out-of-specification batches. Next month’s e-zine will describe how to determine what percentage of material is out of specifications.
Cpk
Cp values are not the best indicators of process capability. The value of Cp does not take into account where the process is centered. Just knowing that a process is capable (Cp > 1.0) does not ensure that all the product or service being received is within the specifications. A process can have a Cp > 1.0 and produce no product or service within specifications. In addition, Cp values can’t be calculated for one-sided specifications. A better measure of process capability is Cpk. This will be introduced in next month’s e-zine.
Summary
This month’s newsletter introduced process capability. The concept of process capability was introduced. Cp was explained with an example of how to calculate the Cp value.