December 2025

This month, we are introducing binary logistic regression. This type of regression is used when there are only two possible outcomes. For example, suppose we are in the medical field and want to determine what predictor variables influence whether a person gets a certain disease. There are only two possible outcomes: the person gets the disease or does not get the disease. Binary logistic regression can be used to build a model for predicting the odds for who will get the disease and who will not, based on the levels of the predictors.
In this issue:
- Introduction
- When to Use Binary Logistic Regression
- Binary Logistic Regression Model
- Example
- Binary Logistic Regression Output
- Summary
- Quick Links
Please feel free to leave a comment at the end of the publication or download a pdf copy of it at this link.
Introduction
There are times when we do not need to predict a numeric value, like % purity or downtime on a machine. Instead, we need to predict a yes/no outcome. Examples include:
- Will a customer default on a loan?
- Will an employee quit?
- Will a piece of equipment fail?
- Will this ad generate a sale?
All these have only two possible outcomes. This leads to a binary response variable – either something happened or it didn’t. And binary logistic regression is used to model this situation.
When to Use Binary Logistic Regression
You can use binary logistic regression under the following conditions:
- The response variable is binary (e.g., yes/no)
- You want to predict the probability of one of those responses based on the predictor variables used in the model.
- The results are independent of one another
Binary Logistic Regression Model
The model for binary logistic regression is:
where p is the probability (between 0 and 1), the b’s are the coefficients of the predictors (X’s). p/(1-p) is called the odds. Using the log of the odds allows the linear relationship among the predictors.
The odds give how likely an event is to occur. If the odds are less than 1, the event is unlikely. If the odds equal 1, then the event is equally likely. If the odds are greater than 1, the event is more likely than not to occur.
Example
A clinic wants to discover what contributes to hypertension. They are looking at 4 predictor variables: age (years), BMI (body mass index), physical activity (hours per week), and stress scorej (higher values mean more stress).
The logistic regression model will estimate the probability that a person has hypertension given their age, BMI, activity level, and stress score. The response variable is 1 if the person has hypertension or 0 if the person does not have hypertension.
The clinic collects data for 120 patients. The data for the first 10 people are shown in Table 1. You can download all the data at this link.
Table 1: Data for Binary Logistic Regression on Hypertension
|
Age |
BMI |
Physical Activity |
Stress Score |
Hypertension |
|
46.90 |
34.10 |
9.40 |
16.60 |
1 |
|
72.80 |
35.90 |
9.50 |
24.30 |
1 |
|
62.90 |
24.40 |
9.10 |
18.70 |
1 |
|
56.90 |
20.20 |
3.70 |
21.40 |
1 |
|
37.00 |
22.60 |
0.20 |
33.20 |
0 |
|
37.00 |
26.50 |
9.30 |
16.60 |
1 |
|
32.60 |
34.40 |
4.30 |
33.80 |
1 |
|
69.00 |
35.20 |
9.70 |
32.20 |
1 |
|
57.10 |
18.10 |
9.60 |
10.90 |
0 |
|
61.90 |
28.20 |
8.50 |
7.10 |
1 |
The data ranges for the 120 persons are given below.
- Age: 30.2 to 74.4
- BMI: 18.1 to 37.7
- Physical Activity: 0.1 to 9.9
- Stress Score: 5.3 to 34.8
The data for the 120 persons was analyzed using the binary logistic regression routine in the SPC for Excel software. The output is described below. You can see more information on the SPC for Excel software at this link.
Binary Logistic Regression Output
Response Summary and Deviance Table
The response summary starts the analysis and is shown in Table 2.
Table 2: Response Summary for Hypertension Data
|
Age |
BMI |
Physical Activity |
|
Response |
Value |
Count |
|
Hypertension |
1 |
76 |
|
0 |
44 |
|
|
Total |
120 |
The response table summarizes how many people in the sample of 120 have hypertension (value of 1) and how many did not have hypertension (value of 0). 76 out of 120 people have hypertension.
Deviance Table
The next portion of the output is the deviance table. This is shown in Table 3.
Table 3: Deviance Table for Hypertension Data
|
Source |
DF |
Deviance |
Mean |
Chi-Square |
p value |
|
Regression |
4 |
43.95 |
10.99 |
43.95 |
0.000 |
|
Age |
1 |
29.90 |
29.90 |
29.90 |
0.000 |
|
BMI |
1 |
24.71 |
24.71 |
24.71 |
0.000 |
|
Physical Activity |
1 |
1.283 |
1.283 |
1.283 |
0.257 |
|
Stress Score |
1 |
0.00929 |
0.00929 |
0.00929 |
0.923 |
|
Error |
115 |
113.8 |
0.989 |
||
|
Total |
119 |
157.7 |
The deviance table for binary logistic regression is calculated the same way as we showed in our SPC Knowledge Base article Poisson regression last month.
The deviance table tells you how well the model fits the data and whether adding each predictor helps improve the model. Deviance measures how far the model predictions are from what is observed. Small deviances are good; large deviances are not good.
The “Deviance” column contains the deviances. The “Total” deviance is the deviance of a model containing no predictors – just models to the average value. This data gives a total deviance of 157.7.
The “Regression” deviance is the improvement from adding all the predictors to the model. Its value is 43.95 in our example. This means that a deviance of 43.95 can be removed from the total deviance of 157.7 by adding all the predictors to the model.
The “Error” deviance gives the deviance unexplained by the model. It is the “Total” deviance – the “Regression” deviance = 157.7 – 43.95 = 113.8.
The columns in the deviance table are:
- DF: Degrees of freedom for that predictor.
- Deviance: How much variation that predictor explains.
- Mean: Deviance divided by DF.
- Chi-Square: Test statistic comparing models with and without that predictor.
- p-value: whether the predictor has a significant effect (usually < 0.05) or not (usually >0.05).
Look at the p-value column. The value of p for regression is < 0.05. This means that the regression is statistically significant. Adding the predictors helped significantly improve the model.
Now look at each of the four predictors. Two of them have p-values < 0.05. These are age and BMI. This means that both predictors have a statistically significant impact on those with hypertension. The other two predictors (physical activity and stress score) do not have a statistically significant impact on hypertension.
The deviance table tells us that the regression and two of the predictors have a significant impact on hypertension.
Predictor’s Table
The predictor’s table is next in the output. There appears to be significant effects by two of the predictors. The predictors’ table helps us begin to quantify the effect. The predictors’ table is shown in Table 4.
Table 4: Predictors’ Table for Hypertension Data
|
Coeff. |
Standard Error |
z Value |
p Value |
95% Lower |
95% Upper |
VIF |
|
|
Intercept |
-10.75 |
2.313 |
-4.648 |
0.0000 |
-15.29 |
-6.219 |
|
|
Age |
0.103 |
0.0225 |
4.572 |
0.0000 |
0.0589 |
0.147 |
1.425 |
|
BMI |
0.214 |
0.0495 |
4.323 |
0.0000 |
0.117 |
0.311 |
1.448 |
|
Physical Activity |
0.0940 |
0.0837 |
1.123 |
0.2614 |
-0.0700 |
0.258 |
1.042 |
|
Stress Score |
-0.0024 |
0.0249 |
-0.0963 |
0.9232 |
-0.0513 |
0.0465 |
1.028 |
The columns in this table are described below.
- Coeff: The coefficient is the effect of the predictor on hypertension. A positive value increases the odds of having hypertension. A negative value decreases the odds of having hypertension.
- Standard Error: gives the variability in the estimate of the coefficient. The smaller the standard error, the more precise the estimate of the coefficient.
- Z Value: coefficient divided by the standard error. A larger value implies the predictor has a significant impact on the outcome.
- p Value: whether the predictor has a significant effect (usually < 0.05) or not (usually >0.05).
- 95% Lower / Upper: This is the 95% confidence interval for the coefficient. If it contains 0, then the predictor is not significant. If the interval does not contain 0, the predictor is significant.
- VIF: measures if the predictors are highly correlated with each other. High values of VIF mean that the two predictors at least are highly correlated. You don’t know which one has the impact. It also leads to other issues. So you want VIF to be around 1.
- No collinearity if VIF = 1
- Moderate collinearity if VIF > 5
- High collinearity if VF > 10
The predictors’ table tell us how much each predictor impacts hypertension. We can now use the information from the predictors’ table to build the model.
Regression Model
The logistic regression can be written as:
This can be rewritten as:
p(Event) = Exp(Y)/(1+Exp(Y))
Y = -10.75 + 0.103(Age) + 0.214(BMI) + 0.094(Physical Activity) – 0.002(Stress Score)
Y is the linear predictor (the log-odds of the event). P(Event) is the predicted probability that the event will occur. In this example, it is the predicted probability that hypertension occurs. The exponential transform converts log-odds into a probability between 0 and 1.
- If Y = 0, then p = 0.5
- If Y > 0, then p > 0.5 (event is more likely)
- If Y < 0 then p < 0.5 (event is more unlikely)
So, the model estimates the probability that a person has hypertension given their age, BMI, physical activity, and stress score.
Suppose we want to predict the outcome for a person with age = 60, BMI = 26, physical activity = 2 and stress score = 30. Putting these values in the equations above gives the following:
P(Event) = 0.752
What does this mean? The 0.752 means that, given age = 60, BMI = 26, physical activity = 2, and stress score = 30, the model predicts a 75.2% probability that the outcome variable equals 1 (i.e., that the modeled event (hypertension) occurs).
Model Stats
The model statistics are shown in Table 5.
Table 5: Model Statistics for Hypertension Data
|
Deviance R Squared |
27.86% |
|
Deviance Adjusted R Squared |
25.35% |
|
AIC |
123.8 |
|
AICc |
124.3 |
|
BIC |
137.7 |
These statistics are measures of how well the model fits the data and how the model compares to other models.
Deviance R Squared: this answers the question about how much of the variation in the response variable is explained by the model. In this example about 28% of the variation is explained.
Deviance Adjusted R Squared: this examines if you have too many predictors. The value is about 25%. Since it is close to the deviance R squared, the model does not have too many predictors.
AIC, AICs, BIC: these are used to compare models with lower values being better. We will not delve into this since we are only considering one model.
Goodness of Fit
The goodness of fit information is shown in Table 6.
Table 6: Goodness of Fit for Hypertension Data
|
Statistic |
DF |
Value |
Mean |
Chi-Square |
p value |
|
Deviance |
115 |
113.8 |
0.989 |
113.8 |
0.5149 |
|
Pearson Chi-Squared |
115 |
129.2 |
1.124 |
129.2 |
0.1724 |
|
Hosmer-Lemeshow |
7 |
3.546 |
0.507 |
3.546 |
0.8303 |
There are three goodness of fit tests in Table 6. The main column to look at is the p-value column. The first test is deviance. The deviance compares the fitted model to a perfectly fitting (saturated) model. The null hypothesis is that the model fits the data. Since the p-value is 0.5149, you conclude that the model fits the data.
The second test is the Pearson chi-squared test. It measures discrepancy between observed and expected outcomes. The p-value is 0.1724. The model fits the data.
The Hosmer–Lemeshow (H–L) test is a goodness-of-fit test specifically designed for binary logistic regression. It checks whether the predicted probabilities from your model agree with the observed outcomes. Since p = 0.803, the predicted and observed outcomes are the same. Again, the model fits the data.
Other Output
There is other output associated with the binary logistic regression technique. There is residuals analysis of the results to look for outliers. There is also the ability to remove predictors and observations. You can also enter the predictor values and predict if the person has hypertension. Please review our SPC Knowledge Base publication on Poisson regression to see this other output.
Summary
This publication has introduced binary logistic regression. This type of regression is used when there is binary outcome, either an event occurs or it does not occur. This publication showed the output for binary logistic regression from the SPC for Excel software for this type of regression. The output includes the deviance table, the predictors’ table and the regression model.

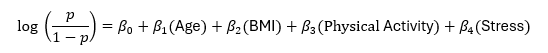
The odds ratio has to be weel explained. In addition, it has to consider more unity in the case of continuous variable.
“The results are independent of one another”
the above sentence is very cryptic ans has to be clarified.