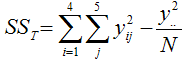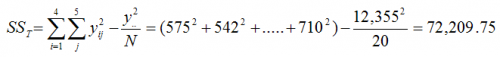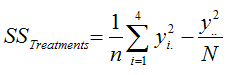December 2008
In This Issue:
- ANOVA Introduction
- ANOVA Table
- Sum of Squares Calculations
- Filling in the ANOVA Table
- Which Treatment Means are Different
- Summary
- Quick Links
As 2008 draws to an end, we want to wish you and yours the best in the coming year. 2008 has been a turbulent year for many on the economic front – the credit fiasco, the housing market burst, layoffs, bailouts – just to name a few. We hope you have been spared the effects of these. Hopefully we will see a turnaround in 2009.
This newsletter also marks a change for us. This is number 60 for us – five years of providing monthly newsletters. Over this time, we have presented a variety of topics related to process improvement through the use of SPC (statistical process control). These topics have included variation, many types of control charts, Pareto diagrams, histograms, scatter diagrams, a problem solving methodology and much more.
We are now expanding the scope of our newsletters to include more statistical topics that are commonly used in process improvement efforts. These topics, for example, will include hypothesis testing, experimental design, ANOVA, nonparametric testing and chi-square tests among others. These topics reflect the expansion of statistical techniques in the new version of our SPC for Excel software. While we will retain the name SPC for Excel, the new techniques are designed to meet the needs of anyone involved in statistical data analysis, particularly those who use Six Sigma as their methodology for improvement. To start this process, we will introduce a commonly used statistical tool: Analysis of Variance. Once again, best wishes in the New Year!
Analysis of Variance (ANOVA) Introduction
Earlier newsletters show how to compare two different processes or treatments. Many times you will want to compare more than two processes. ANOVA provides a method of doing this. In this newsletter, we will look at single factor ANOVA where we want to compare the results for different levels (treatments) of the factor.
We will use an example from the excellent book Design and Analysis of Experiments, 6th Edition, by Douglas C. Montgomery. The example involves a plasma etching process. An engineer wants to determine if there is a relationship between the power setting and the etch rate. She is using four different power settings (160W, 180W, 200W and 220W). The engineer tested five wafers at each power level. The data from the experiment are shown below.
| Treatment/Power | 160 | 180 | 200 | 220 |
| 1 | 575 | 565 | 600 | 725 |
| 2 | 542 | 593 | 651 | 700 |
| 3 | 530 | 590 | 610 | 715 |
| 4 | 539 | 579 | 637 | 685 |
| 5 | 570 | 610 | 629 | 710 |
The experiments were run in random order. The four power settings are the column headings. The results for each of the five wafers from each setting are below the headings. For example, when the power setting was 160, the five etch rates obtained were 575, 542, 530, 539 and 570.
ANOVA Table
The ANOVA table has the following basic form.
| Source | Sum of Squares | Degrees of Freedom | Mean Square | F Value |
| Between Treatments | SSTreat | a – 1 | SSTreat/(a-1) | MSTreat/MSE |
| Error (Within Treatments) | SSError | N – a | SSError/(N-a) | |
| Total | SSTotal | N – 1 |
The first column contains the source of variation. It divides the sources of variation into two major categories: within treatment (error) and between treatment. The objective is to determine if there are any differences between treatments (in this example, the different power settings). This is done by comparing the between treatments sum of square (variance) to the error sum of square (variance). If the variance between treatments can be explained by the within treatment variance, we will conclude that there are no differences between the treatments. If the variance between treatments cannot be explained by the within treatment variance, we will conclude that there are differences between the treatments.
The second column in the table contains the sum of squares. These are calculated variances as shown below.
The third column is the degrees of freedom. The number of levels is given by a. N is the total number of experimental runs.
The fourth column is the mean square. The mean square is obtained by dividing the sum of squares for the source by the degrees of freedom for the source. Thus, MSE = SSError/(N-a).
The fifth column is the F value. This is determined by dividing the mean square for the treatments by the mean square error. It is this value that determines if there are any significant differences between the treatment means.
We will now determine the sum of squares for each source of variation.
Sum of Squares Calculations
The sum of squares calculations for the three sources in the ANOVA table are shown below. The information in the table below is helpful for the calculations.
| Treat/Power | 160 | 180 | 200 | 220 |
| 1 | 575 | 565 | 600 | 725 |
| 2 | 542 | 593 | 651 | 700 |
| 3 | 530 | 590 | 610 | 715 |
| 4 | 539 | 579 | 637 | 685 |
| 5 | 570 | 610 | 629 | 710 |
| Totals | 2756 | 2937 | 3127 | 3535 |
The total sum of squares is given by the following:
where yij is for the jth sample for the ith treatment level, N is the total number of experimental runs (20 in this example) and y2.. is the square of the sum of all of the experimental run results (12,355 in this example).
The treatment sum of squares is given by the following:
where n is the number of observations per treatment level and yi. is the total for each treatment level.
The sum of squares for the error is simply the difference between the total and treatment sum of squares.
SSError = SSTotal-SSTreatments = 72,209.75 – 66,870.55 = 5339.20
Filling in the ANOVA Table
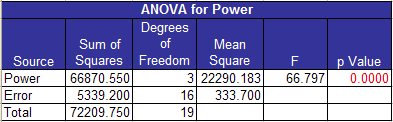
The rest of the ANOVA table can now be filled in. The ANOVA output from the software is shown below for this example.
The degrees of freedom for power (the treatments) is the number of treatment levels (4) minus 1 = 3. The error degrees of freedom is the total number of runs (N) minus the number of treatment levels (a): N – a = 20 -16 = 4. The total degrees of freedom is N minus 1 = 19.
The mean square column is found by dividing the sum of squares for the source by the degrees of freedom for the source. Thus:
MSPower = 66,870.55/3 = 22,290.18
MSE = 5339.20/16 = 33.70.
Note that the MSE is much smaller than the MSpower. This means the within treatment (error) variation is much smaller than the between treatment (power) variation. The greater this difference, the more likely there is a significant difference in the treatment levels. The F value is used to determine the magnitude of the difference:
F = MSPower/MSE = 22,290.18/333.70 = 66.80.
To determine if this value of F is “significant”, i.e., there is a significant difference in the treatment levels, you can compare this value of F to a table value of F (the critical F value). The F distribution is used for this. Values of the F distribution for different values of alpha and degrees of freedom are in many statistical books. You can also use FINV function in Excel. For alpha = 0.05 and 3 degrees of freedom for the treatments and 16 degrees of freedom for the error, the critical value of F is 3.24. If the calculated value of F is greater than the critical value, there is a significant difference between the treatment levels. Since 66.80>3.24, we conclude that there is a significant difference in the treatment levels.
Most software packages (including ours) give a p value associated with the F value. This is the probability of obtaining the calculated F value (66.80) if there were in fact no difference between the treatment levels. If p is less than 0.05, we usually conclude that there is a significant difference. In this example, p is less than 0.0001.
Which Treatment Means are Different
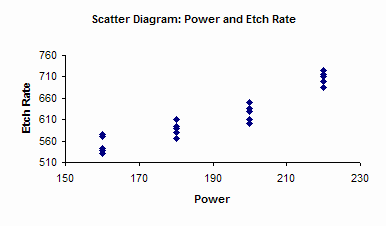
The ANOVA table simply tells you that the treatment levels are significantly different. It doesn’t tell you which ones are significantly different. More analysis is needed for this. One method is to create a scatter diagram. This chart from the software is shown below. The results are plotted versus power level. You can easily see that the etch rate increases as the power level increases.
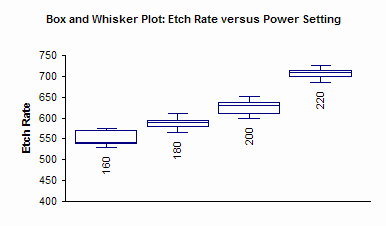
You can also do a Box and Whisker chart for the data (click here for more information on Box and Whisker charts).
Additional analysis that can be done includes developing confidence intervals for each pair of treatment means as well as applying the Fisher’s LSD method, Tukey’s Method or Bonferroni’s method for determining if significant differences exist between treatment means. You can also apply Bartlett’s or Levene’s test for equality of variances. These techniques are in the new version of the software. Next month’s newsletter will examine one of the three methods for determining which treatment means are significantly different from others.
Summary
This month we introduced the single factor ANOVA. This type of analysis is designed to determine if levels of a single factor impact a response variable. The ANOVA table was developed along with the calculations required. The scatter diagram and Box-Whisker plot were used to graphically show which levels could be different. Next month, we will look at a mathematical way to determine which levels are significantly different.