April 2007
In this issue:
Control charts work very well the vast majority of times. A control chart will tell you if everything in the process is operating as the process was designed and is managed on a day to day basis (only common causes present). Or, a control chart will tell if you have a problem in the process (a special cause).
It is a pretty fail-safe method of monitoring a process. When a chart does fail, it usually hides a special cause of variation. Very seldom does a control chart send a false signal, i.e., that a special cause exists when in fact there is only common cause of variation. One time this does happen, though, is when you have large differences in the measurement results. This is called “chunky” data. This publication examines this type of data and the impact it has on control charts.
Variation Review
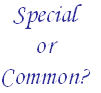
If you understand variation, you will realize that most of the problems you face are not due to individual people but to the process — the way it was designed and the way it is managed on a day-to-day basis.
Variation comes from two sources: common and special causes. Think about how long it takes you to get to work in the morning. Maybe it takes you 30 minutes on average. Some days it may take a little longer; some days a little shorter. But as long as you are within a certain range, you are not concerned. The range may be from 25 to 35 minutes. This variation represents common cause variation — it is the variation that is always present in the process. And this type of variation is consistent and predictable. You don’t know how long it will take tomorrow to get to work, but you know that it will be between 25 and 35 minutes as long as the process remains the same.
Now, suppose you have a flat tire when driving to work. How long will it take you to get to work? Definitely longer than the 25 to 35 minutes in your “normal” variation. Maybe it takes you an hour longer. This is a special cause of variation. Something happened that was not supposed to happen. It is not part of the normal process. Special causes are not predictable and are sporadic in nature.
Why is it important to know the type of variation present in your process? Because the action you take to improve your process depends on the type of variation present. If special causes are present, you must find the cause of the problem and then eliminate it from ever coming back if possible. This is usually the responsibility of the person closest to the process. If only common causes are present, you must FUNDAMENTALLY change the process. The key word is fundamentally — a major change in the process is required to reduce common causes of variation. And management is responsible for changing the process. For more information on variation and Dr. Deming, please see our archived newsletters on our website.
Control Charts
The only way to determine if a process has special causes of variation present or just has common causes of variation is through the use of control charts. A control chart is a picture of your process.
In a control chart, the points are plotted over time. An average line is calculated along with an upper control limit and a lower control limit. The upper control limit is the largest value you would expect if there is just common cause of variation present in the process. The lower control limit is the smallest value you would expect. The limits are determined by mathematical equations. They depend on the type of control chart and how you sample the process.
A process is in “statistical control” if it has only common cause of variation present. This is determined by examining the control chart. As long as the chart has no points above or below the control limits or no patterns (such as seven points in a row above or below the average), the process is said to be in statistical control.
You can predict what will happen with a process that is in control. Future production will continue between the two limits as long as the process remains the same.
To effectively use control charts, you must be able to interpret them. Ask: What is this chart trying to tell me about my process? A control chart is the way a process communicates with you. It will tell you if the process is operating as designed (in control) or if there is a problem (special cause). All you have to do is “listen.”
The Problem with Chunky Data
Control charts work, plain and simple. At least most of the time. They are not totally fail-safe. If a control chart does fail, it usually fails by hiding a problem. That is, there is a special cause of variation present and it does not show up on the control chart as an out-of-control point. Seldom does a control chart give you a false alarm – indicating an out-of-control point when it is actually a common cause of variation.
There is one exception to this. Dr. Donald Wheeler calls this exception “chunky” data. Chunky data occurs when the range between possible values becomes too large. The example Dr. Wheeler cites is measuring a person’s height to the nearest yard. This measurement is too large and would obscure the variation in height from person to person. Excessive round-off will lead to chunky data. It can also occur when the measurement process cannot tell the difference between samples (usually indicated by a very large gage R&R %). In this case, the measurement unit is too large (as in the case of measuring a person’s height to the nearest yard).
Suppose you have a process with a quality characteristic that averages about 100. You collect 40 samples from the process and construct an individuals control chart (X-mR). Please see our October 2006 e-zine on the website for information on constructing individuals control charts. The data you collected are given below.
| 99.08 | 99.5 | 99.49 | 100.43 | 99.95 | 100 | 100.48 | 99.91 |
| 99.45 | 99.71 | 100.86 | 100.13 | 100.11 | 99.39 | 99.23 | 100.15 |
| 100.04 | 99.72 | 100.71 | 99.75 | 100.39 | 100.14 | 99.71 | 99.84 |
| 100.35 | 100.54 | 100.15 | 100.32 | 99.94 | 100.24 | 100.45 | 100.2 |
| 99.33 | 99.58 | 100.11 | 100.19 | 99.89 | 99.79 | 99.81 | 100.06 |
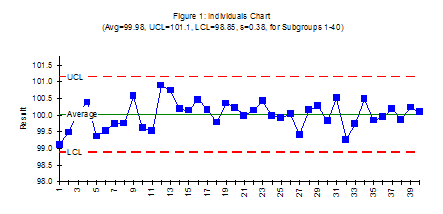
The control chart for this data is shown in the figure below. Figure 1 is the X chart; figure 2 is the moving range chart. Note that this process is in statistical control (see our April 2004 publication on how to interpret control charts). There are no points beyond the control limits and no patterns such as seven points in a row above or below the average. The process is consistent and predictable. We know what it will produce in the future as long as the process stays the same.
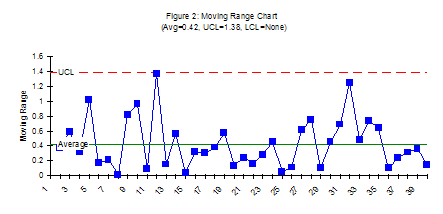
Now suppose that instead of using a measurement system that went to two decimal places, you replace it with one that rounds off to the nearest integer. Rounding the data to the nearest data point leads to the following data:
| 99 | 100 | 99 | 100 | 100 | 100 | 100 | 100 |
| 99 | 100 | 101 | 100 | 100 | 99 | 99 | 100 |
| 100 | 100 | 101 | 100 | 100 | 100 | 100 | 100 |
| 100 | 101 | 100 | 100 | 100 | 100 | 100 | 100 |
| 99 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
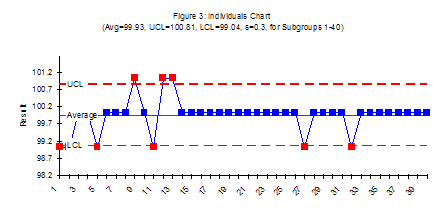
The control charts for this data is shown in the figure below. Figure 3 is the X chart. Figure 4 is the moving range chart. Note that there are eight out-of-control points on the X chart and one out-of-control point on the moving range chart. These out-of-control points occurred simply because of the way we rounded the number. They have nothing at all to do with the process – which we showed was in control with the first chart. They are the result of excessive rounding which produces what Dr. Wheeler calls chunky data. This type of data can lead to false alarms. You will get out-of-control points when the process is actually in control (consistent and predictable).
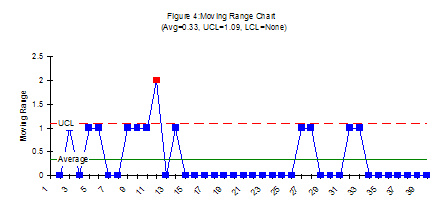
Identifying Chunky Data
Quite often, the cause of chunky data will be the measurement process. For example, one company was measuring the time it took shipments from a given supplier to arrive. The time was rounded off to days. This led to the type of chart seen above. Out-of-control points were actually due to the measurement process. How can you identify chunky data? It is easy. You look at the range chart. This is one of the best reasons for doing a moving range chart. Count the number of possible values below the upper control limit. In the second example above, there are only two possible values below the upper control limit (0 and 1). Compare that to the first example above where you can have values between 0 and 1.37 in increments of 0.01 (137 possible values). There are many more possible values with the first example than the second. This is how you tell if you have chunky data. The general rules presented by Dr Wheeler are given below.
- For Xbar-R charts: the data is chunky is the range chart has four or fewer possible values below the upper control limit.
- For X-mR charts: the data is chunky if the range chart has three or fewer possible values below the upper control limit.
If you have chunky data, you will, in most cases, need to look at improving the measurement process.
Summary
This month’s publication looked at how “chunky” data can impact an individuals control chart. Chunky data often occurs with excessive round-off. An example of data with and without excessive roundoff was shared to show what happens to the individuals control chart. Essentially, there are many “false” out of control points with chunky data. The range chart can be used to help determine if you have chunky data.