April 2005
In this issue:
This month is the second in a multi-part publication on X-R charts. Last month we introduced the chart and provided the steps in constructing an X-R chart. This month, we will look at a detailed example of an X-R chart. The X-R chart is a type of control chart that can be used with variables data. Like most other variables control charts, it is actually two charts. One chart is for subgroup averages ( X). The other chart is for subgroup ranges (R). These charts are a very powerful tool for monitoring variation in a process and detecting changes in either the average or the amount of variation in the process.
Bag Weight Process
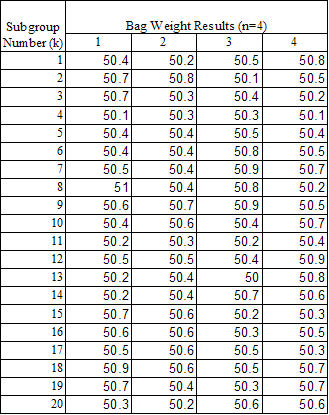
A process involves the filling of bags with sand. Each bag is supposed to weigh a minimum of 50 pounds. The process has an automatic method of weighing the bags. Once the bag reaches 50 pounds, the filling operation is supposed to stop. To determine how much variation there is in the bag weights, an operator takes the first four bags filled each hour and manually weighs them using a calibrated scale. The data are shown in the table.
We want to use an X-R chart to find out if this process is consistent and predictable (in control) as well as if it is capable of producing bag weights with a minimum of 50 pounds.
The calculations needed to construct the X-R chart were covered in last month’s e-zine. For practice, you can copy the data from this e-zine into Excel and see if you can get the same results as shown below. The subgroup size is 4. For the data above, the following averages and control limits can be generated.
For the X chart:
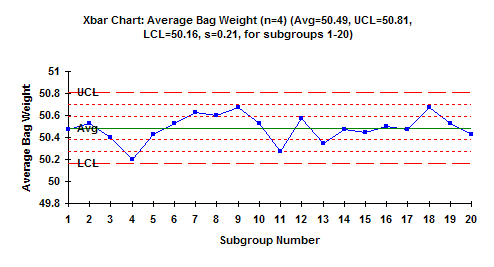
Average = 50.49
UCL = 50.81
LCL = 50.16
For the range chart:
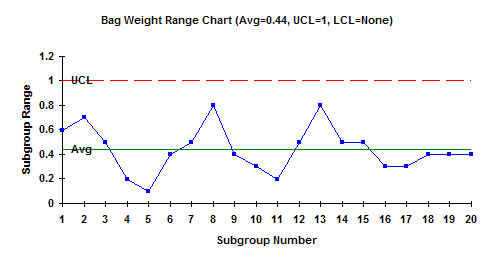
Average = 0.44
UCL = 1.00
LCL = None
The X-R charts are shown below. Are these charts in control? For information on interpreting control charts, please see our past publication on our website. Interpreting control charts was covered in April 2004.
X-R Chart
Interpreting the Charts
The X and R charts above are in statistical control. This means that the process is consistent and predictable. There are only common causes of variation present (see the January 2004 e-zine on variation for more information on common and special causes of variation).
What does it mean for a range chart to be in statistical control? It means that variation within the subgroup is consistent from subgroup to subgroup. For the bag weight example, it means that the range between the heaviest bag and lightest bag is the “same” for all bag weights. There is no statistical difference between these ranges. The average range will be 0.44 pounds but it can vary anywhere from 0 to 1 pounds. Since the range chart is in control, you can estimate the standard deviation using the formula provided in last month’s e-zine. The standard deviation is 0.21
What does it mean for the X chart to be in statistical control? It means that the variation between subgroup averages is the same from subgroup to subgroup. For the bag weight example, it means that there is no statistical difference between the subgroup averages. As long as the process stays the same, we can predict the average bag weights for the four samples. The long-term average will be 50.49. The average will vary from 50.16 to 50.81.
Is the Process Capable?
Can the process meet the specification of having a minimum bag weight of 50? Be careful here. The X chart plots the subgroup averages. The LCL on the X chart is 50.16. This means that the average of the four bag weights will not be below 50.16 as long as the process stays the same. However, the specification deals with individual bag weights, not averages. Individual values will vary more than the subgroup averages. Just because you do not have any subgroup averages below 50, does not mean that you will not have any individual bag weights below 50.
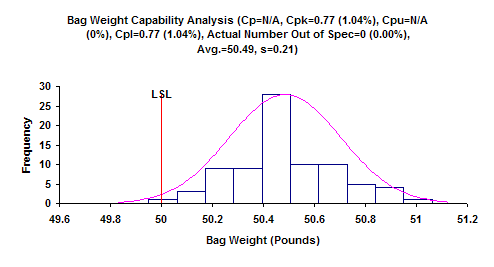
Information process capability is given on our website. We have a three-part series on process capability. The process capability chart for the bag weight process is shown in the figure above. What can you conclude about the process capability?
Note that the data in the table do not have any bag weights below 50. However, the process capability analysis shows that the Cpk = 0.74. Since this is less than 1, it means that there is out-of-specification material – some bags will weigh less than 50 pounds. The analysis predicts about 1% of the bags will weigh less than 50 pounds. The only way to prevent any underweight bags from going to the customer with the current process is to inspect 100% of the bags. Of course, the best approach would be to improve the process – to move the average higher or reduce the amount of variation – so no bags will be produced that weigh less than 50 pounds.
Summary
This publication showed how to create an X-R chart using bag weights as an example. The process was in statistical control. Being in statistical control does not mean that the process is capable. The process capability chart showed that the process was not capable. To make it capable, the process has to be fundamentally change.