In This Issue:
- Variation: Spilling the Milk
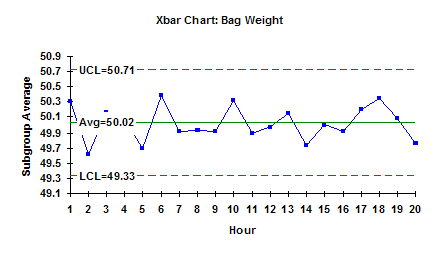
- A Case Study in Variation
- Separating Special from Common Causes
- Alcohol Related Traffic Fatalities: 1982 – 1993
- Alcohol Related Traffic Deaths: 1994 – 2004
- Summary
- Quick Links
Greetings,
This issue takes us back to where everyone who is dealing with statistical process control needs to begin – with variation. To effectively use SPC, you must understand the concept of variation, and in particular, the difference between common and special causes of variation. This is the third time we have presented variation. We will look at a case study that involved truly understanding the concept of variation. And finally, we will apply our knowledge of variation to the issue of alcohol-related traffic fatalities in the United States.
Variation: Spilling the Milk

Variation comes from two sources: common and special causes. Think about how long it takes you to get to work in the morning. Maybe it takes you 30 minutes on average. Some days it may take a little longer, some days a little less. But as long as you are within a certain range, you are not concerned. The range may be from 25 to 35 minutes. This variation represents common cause variation – it is the variation that is always present in the process. And this type of variation is consistent and predictable. You don’t know how long it will take tomorrow to get to work, but you know that it will be between 25 and 35 minutes as long as the process remains the same.
Now, suppose you have a flat tire when driving to work. How long will it take you to get to work? Definitely longer than the 25 to 35 minutes in your “normal” variation. Maybe it takes you an hour longer. This is a special cause of variation. Something happened that was not supposed to happen. It is not part of the normal process. Special causes are not predictable and are sporadic in nature.
Why is it important to know the type of variation present in your process? Because the action you take to improve your process depends on the type of variation present. If special causes are present, you must find the cause of the problem and then eliminate it from ever coming back if possible. This is usually the responsibility of the person closest to the process. If only common cause are present, you must FUNDAMENTALLY change the process. The key word is fundamentally — a major change in the process is required to reduce common causes of variation. And management is responsible for changing the process.
It has been estimated that 85 to 94% of the problems a company faces are due to common causes; only 6 to 15% due to special causes (that may or may not be people related). So, if you always blame problems on people, you will be wrong at least 85% of the time. It is the process most of the time that needs to be changed. Management must set up the system to allow the processes to be changed.
So, Mom, sorry. But most of the time, spilling the milk was not my fault. It was usually yours (management). The glasses were too big for my small hands (no spill-proof cups in those days). When I wanted to put it by the edge of the table to make it easier to reach, you said move it back because I might spill it. And with the meal-time conversation, how could I concentrate on my milk?
So, first teach the concept of variation. Then the use of control charts (see Separating Common from Special Causes below) will make more sense to people.
A Case Study in Variation
To really understand variation, many people have to change their paradigm. The following is a true story. A plant produced a number of different powdered products. Each of these products was run through the same production equipment at different conditions and put into unique silos (one or more for each product type).
To ensure that the product went to the correct silo, an operator had to set up the lines from the process to the correct silo. If product was introduced into the wrong silo, the entire silo had to be sold as off- grade, at a tremendous reduction in price. The cost was typically $30,000 per incident.
The plant leadership had a policy that anyone who cross-contaminated a silo received three days off with no pay. What type of variation did leadership assume was present? Special cause. They assumed that the operators were at fault. One manager said that he was not going to “idiot proof” the plant.
Was leadership correct? The only way to find out was to collect data.
It turned out that anyone who had worked in the unit for more than three months had time off for cross-contaminating a silo. If everyone is doing it, what type of variation is it? Common cause. And the only way to reduce common cause of variation is to change the process.
Leadership put together a team that worked on the problem. The team came up with two simple solutions: label the lines and put better lights out at night. Easy solutions but beyond the authority of the operators to get done by themselves. With the solutions implemented, the problem, which had been occurring almost monthly, went away entirely. So simple if you understand variation.
Separating Special from Common Causes
Control charts are the only reliable way to separate common from special causes of variation. In a control chart, the points are plotted over time. An average line is calculated along with an upper control limit and a lower control limit. Some charts do not have a lower control limit. The upper control limit is the largest value you would expect if there is just common cause of variation present in the process. The lower control limit is the smallest value you would expect. The limits are determined by mathematical equations. They depend on the type of control chart and how you sample the process.
A process is in “statistical control” if it has only common cause of variation present. This is determined by examining the control chart. As long as the chart has no points above or below the control limits or no patterns (such as seven points in a row above or below the average), the process is said to be in statistical control. You can predict what will happen with a process that is in control. Future production will continue between the two limits as long as the process remains the same.
To effectively use control charts, you must be able to interpret the control chart. Ask: What is this chart trying to tell me about my process? A control chart is the way a process communicates with you. It will tell you if the process is operating as designed (in control) or if there is a problem (special cause). All you have to do is “listen.”
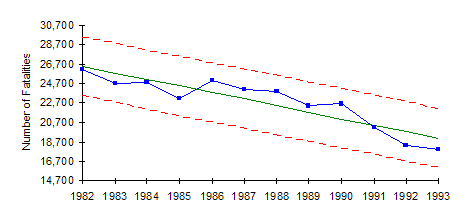
Alcohol Related Traffic Fatalities: 1982 – 1993
The key point is that the statistics you see day in and day out must be interpreted in the context of the process that generated them. Was that process in control and stable? Or did it have special causes of variation present – flat tires? If it had special causes present, you would not get a similar result next time because you cannot predict what a process with special causes of variation will do in the future.
Over the years, many organizations have worked to reduce the number of alcohol-related fatalities in the United States. These organizations range from MADD (Mothers Against Drunk Driving) to the government to the alcohol producers themselves. Improved awareness and new laws have resulted. From 1982 through 1993, the impact was significant. In fact, if you chart the number of alcohol related deaths per year during that time period, you will get a significant downward trend from 26,173 deaths in 1982 to 17,908 in 1993, all while the number of motorists was increasing. This chart is shown below.
But things have changed since then. That significant trend is no longer apparent. What does this mean in light of the material presented above? The data from 1982 to 2004 (the last year that data were available) is given below (source: National Highway Traffic Safety Administration FARS data).
| Year | Deaths |
| 1982 | 26,173 |
| 1983 | 24,635 |
| 1984 | 24,762 |
| 1985 | 23,167 |
| 1986 | 25,017 |
| 1987 | 24,094 |
| 1988 | 23,833 |
| 1989 | 22,424 |
| 1990 | 22,587 |
| 1991 | 20,159 |
| 1992 | 18,290 |
| 1993 | 17,908 |
| 1994 | 17,208 |
| 1995 | 17,732 |
| 1996 | 17,749 |
| 1997 | 16,711 |
| 1998 | 16,673 |
| 1999 | 16,572 |
| 2000 | 17,380 |
| 2001 | 17,400 |
| 2002 | 17,524 |
| 2003 | 17,150 |
| 2004 | 16,694 |
Based on these data, ABC News reporter Ken Thomas reported the following on ABC’s website on August 1, 2005:
WASHINGTON Aug 1, 2005 (AP)- Traffic deaths declined and fewer people were killed in alcohol-related crashes on U.S. highways for a second straight year, the government said Monday. Some 42,636 people died on the nation’s highways in 2004, a reduction of 248 or 0.6 percent from the previous year, the National Highway Traffic Safety Administration said. Alcohol-related fatalities dropped 2.4 percent, from 17,150 in 2003 to 16,694 in 2004. Safety groups attributed the decrease to all 50 states moving toward a uniform standard for drunken driving and to high-visibility enforcement such as sobriety checkpoints.
The last statement implies that the actions sited have helped decrease the number of alcohol-related deaths over the past three years. The average for the years 2002-2004 was 17,123. Has the process really changed? Is this a valid average for the process?
Alcohol Related Traffic Deaths: 1994 – 2004
The only way to answer that question is through the use of control charts. The control chart based on the number of alcohol-related deaths is shown here. Since 1994, the process is in control. The fact that the number has decreased in the last three years doesn’t appear to be unusual. In fact, there was another three-year downward trend from 1997 to 1999, in which there were even fewer fatalities.
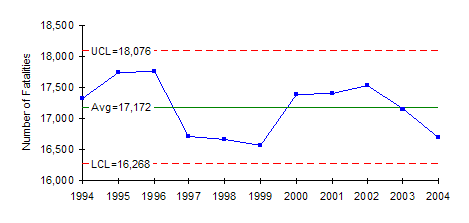
What does the control chart tell us? It tells us, based on the data, that there does not appear to be any significant change in the past three years in the number of alcohol-related deaths. The process is consistent and predictable. If you want to improve the results, you must fundamentally change the process. The key word here is fundamentally. Continuing to try the same type of remedies probably will not work. Significant changes are needed.
What is an example of a significant change? First, realize that the laws are set up to be effective only after the crime. A blood content of 0.08 or more means you are drunk and should not be driving –after the fact. The sobriety checkpoints may catch a drunk driver — again, after the fact.
A significant change would be to install a device in all vehicles that requires you to prove you are sober (or competent) enough to drive a car. Peter McWilliams, in his book Ain’t Nobody’s Business if You Do suggests a tester.
“Imagine a panel on the dashboard with a numeric keypad, like those on touch-tone telephones. Above the keypad is a screen to display numbers and brief messages. There is also a slot, about the size of a credit card. The Tester works like this: When you want to use the car, first insert your driver’s license, which would act and look like a credit card. The Tester reads your driver’s license as an automated teller machine reads your credit card, and then asks for your four-digit personal identification number (PIN), much as a teller machine would. Your PIN is known only to you, but is encoded in your license. After your four-digit personal identification number is successfully given, the screen displays seven random numbers-the number of digits in a phone number. You must then, within a certain period of time and with a certain degree of accuracy, enter those numbers on the keypad. Once you complete this procedure, which should take less than a minute, the car is ready to operate normally.”
This would be a significant change. This is the key. To improve a process that is in statistical control, the process must be fundamentally changed.
Summary
When presented with data, the first question you should ask is, “What is the state of control of the process that generated these data? Is it in control or are there special causes present?” The answer to this will tell you what you need to do to improve your process. If there are special causes present, you have to find the root cause of the problem. If there are only common causes present, you must fundamentally change your process to reduce variation.