September 2018
(Note: all the previous SPC Knowledge Base in the experimental design category are listed on the right-hand side. Select this link for information on the SPC for Excel software.)

You accomplish this by using experimental design techniques. An experimental design is a planned experiment to determine, with a minimum number of runs, what factors have a significant effect on a product response and how large the effect is to find the optimum set of operating conditions.
This month’s publication examines two-level fractional factorial experimental designs. This type of design is useful when you want to examine 4 or more factors. With fewer factors, you can perform a full factorial experimental design. In this publication:
- Experimental Design Terminology Review
- Two-Level Full Factorial Design Review
- Main Effects and Interaction Review
- Design Table Review
- Analysis of Experimental Design Results
- Fractional Factorial Design Layout
- Design Resolution
- Summary
- Quick Links
Please feel free to leave a comment below. You may also download a pdf copy of this publication here.
Experimental Design Terminology Review
There are four previous articles dealing with experimental design in our SPC Knowledge Base. We will review some of the material below but, if you want more information, you can access these articles here. Below are some of the terms used in experimental design.
A factor is a variable over which there is direct control. It is the independent variable in statistical terms. Examples of factors include reaction temperature, reaction pressure, residence time, flow rate, different operators, different shifts, different raw materials, and different lots.
The level of a factor refers to the value of the factor used in an experimental run. For example, if reactor pressure is a factor used in an experiment, two possible levels are 150 PSIG and 200 PSIG.
Fixed factors are factors whose levels in an experiment are set at particular values. The above example of reaction pressure with levels of 150 PSIG and 200 PSIG is an example of a fixed factor. There are also random factors.
A response is a variable whose value depends upon the levels of the factors. It is the dependent variable in statistical terms. Examples of responses include yield, reactor run times, and final product characteristics such as purity, color, density, etc. Cost is also a response variable.
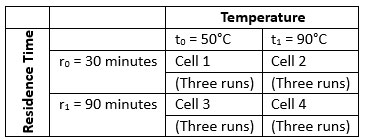
To further develop the terminology associated with experimental design, consider a stirred batch reactor example. Two factors, reactor temperature and residence time, are thought to impact the product purity obtained in a chemical reaction. A planned experiment to investigate this could take the form shown in Table 1. This is a two-level full factorial design.
Table 1: Experimental Design
A treatment or treatment combination is represented by one cell. For example, in cell 1, the treatment is temperature = 50°C and residence time = 30 minutes. A treatment represents the levels of all factors used in a given experimental run. For this experimental design, there are four treatments (r0t0, r0t1, r1t0, and r1t1).
For this experiment, each treatment is run three times. This is called replication of the treatment. Replication is used to estimate the experimental error (the variation in the process). Experimental error is represented by the difference in experimental runs with the same factor levels. For example, the treatment represented in cell 1 above is run three times. The variation in the product purity for these three runs is caused by experimental error. Experimental error is not a very good term for this. It is actually measuring the process variation.
This process variation will be used to determine if a factor has a significant effect on a response. If the differences seen in the response variable due to different levels of the factor can be explained by normal process variation, we will conclude that the factor does not affect the response. However, if the differences cannot be explained by normal process variation, we will conclude that the factor does affect the response.
Two-Level Full Factorial Design Reviews
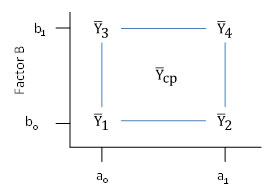
A full factorial design runs every possible combination of factor levels. The simplest full factorial design is the 22 design, such as the reactor example above. The first two in the 22 design represents the number of levels while the exponent represents the number of factors. The factor space (a square for two factors) for a 22 factorial design is given in Figure 1. The factor space is the region surrounded by the experimental runs.
Figure 1: 22 Factorial Design Factor Space
There are two factors, A and B. The low levels are given by a0 for factor A and by b0 for factor B. The high levels are given by a1 for factor A and b1 for factor B. The average responses are indicated by Yi for treatment condition i. Ycp represents runs that may be made at the center point of the square. The center point runs are optional and can be used to either estimate process variation or to determine if there is curvature in the factor space.
Main Effects and Interactions
A full factorial design allows you to estimate the effect of all factors and their interaction on the response. The main effect describes how a factor influences the product response. This influence, however, sometimes depends on the levels of the other factors. This is called interaction. The full factorial above will estimate the effect of Factor A, Factor B and the interaction AB.
Design Table Review
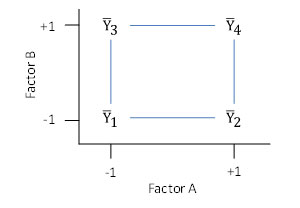
Design tables are commonly used to show the treatment conditions for an experimental design. To understand how to set up a design table, we will use “coded” factor levels. When a factor is at its low level, it is represented by a -1. When a factor is at is high level, it is represented by a +1. This situation is shown in Figure 2.
Figure 2: Use of Coded Factor Levels to Develop a Design Table
The numbering of the cells (1 through 4) is a standard numbering system (called Yates’ run order) used in experimental designs. The design table for this example is given in Table 2.
Table 2: Design Table for a 22 Factorial Design
| Run | Mean | A | B | AB |
|---|---|---|---|---|
| 1 | + | – | – | + |
| 2 | + | + | – | – |
| 3 | + | – | + | – |
| 4 | + | + | + | + |
For run 1, both factors are at their low level (-1). Thus under A and under B, a – sign is placed (the 1 is dropped for convenience). The sign under AB is determined by multiplying the level of A by the level of B, i.e., (-1)(-1) = +1. Thus, a + sign is placed under the AB column for Run 1.
The same approach is used for Runs 2 – 4. The mean column has only pluses.
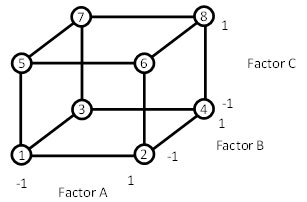
The factor space for a three-factor two-level factorial design is a cube as shown in Figure 3.
Figure 3: Factor Space for 23 Experimental Design
The design table for three factors is shown below. This type of design will estimate the effects of the three factors (A, B, C), the three two-factor interactions (AB, AC, BC), and the three-factor interaction (ABC).
Table 3: 23 Factorial Design Table
| Run | Mean | A | B | AB | C | AC | BC | ABC |
|---|---|---|---|---|---|---|---|---|
| 1 | + | – | – | + | – | + | + | – |
| 2 | + | + | – | – | – | – | + | + |
| 3 | + | – | + | – | – | + | – | + |
| 4 | + | + | + | + | – | – | – | – |
| 5 | + | – | – | + | + | – | – | + |
| 6 | + | + | – | – | + | + | – | – |
| 7 | + | – | + | – | + | – | + | – |
| 8 | + | + | + | + | + | + | + | + |
Analysis of Experimental Design Results
Analysis of Variance (ANOVA) techniques are used to determine what main effects and interactions significantly impact the response variable. We will review this in our next publication when we present examples of fractional factorial designs.
Fractional Factorial Design Layout
There is a significant drawback to full factorial designs. As the number of factors increases (k), the number of runs (N) for a full 2k factorial design increases rapidly. For example, if you have 3 factors, the minimum number of runs for full factorial is 23 = 8. This is without any replication. If you replicate the design twice, the number of runs increases to 16. For 4 factors, the minimum number of runs for a full factorial design is 24 = 16 and for 5 factors it is 25 = 32. As the number of factors increase, the number of runs needed for full factorial design increases very rapidly – usually beyond what is reasonable to do.
But there is a solution to this problem. When the number of factors becomes too large, the desired information can often be obtained by performing only a fraction of the full factorial design – hence the name fractional factorials.
Full factorial designs provide estimates of all the main effects and interactions. For example, if k=2, a full factorial provides estimates of the average, two main effects and one two-factor interaction. If k=7, the 128 run full factorial provides estimates of the average, seven main effects, 21 two-factor interactions, 35 three-factor interactions, 35 four-factor interactions, 21 five-factor interactions, 7 six-factor interactions and 1 seven-factor interaction. Wow, lots of information.
The fact that all these effects can be estimated doesn’t mean that they are all significant. There tends to be a hierarchy of effects. In general, main effects are more significant than two-factor interactions which are more significant than three-factor interactions, etc.
Quite often at some point, the higher order interactions tend to become insignificant and can be ignored. In addition, not all factors in a design with many factors will be significant. Thus, if k is large, there tends to be a redundancy in a full factorial design. This redundancy is due to the excess number of interactions that can be estimated and sometimes an excess number of factors that are studied. Why should we waste time and money estimating effects and interactions that are probably insignificant? Fractional factorial designs exploit this redundancy found in full factorials when k is large.
Anytime there are four or more factors, a fractional factorial design should be considered. The design table for a 24 factorial design is shown below.
Table 4: 24 Full Factorial Design Table
| Run | Mean | A | B | C | D | AB | AC | AD | BC | BD | CD | ABC | ABD | ACD | BCD | ABCD |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| *1 | + | – | – | – | – | + | + | + | + | + | + | – | – | – | – | + |
| 2 | + | + | – | – | – | – | – | – | + | + | + | + | + | + | – | – |
| 3 | + | – | + | – | – | – | + | + | – | – | + | + | + | – | + | – |
| *4 | + | + | + | – | – | + | – | – | – | – | + | – | – | + | + | + |
| 5 | + | – | – | + | – | + | – | + | – | + | – | + | – | + | + | – |
| *6 | + | + | – | + | – | – | + | – | – | + | – | – | + | – | + | + |
| *7 | + | – | + | + | – | – | – | + | + | – | – | – | + | + | – | + |
| 8 | + | + | + | + | – | + | + | – | + | – | – | + | – | – | – | – |
| 9 | + | – | – | – | + | + | + | – | + | – | – | – | + | + | + | – |
| *10 | + | + | – | – | + | – | – | + | + | – | – | + | – | – | + | + |
| *11 | + | – | + | – | + | – | + | – | – | + | – | + | – | + | – | + |
| 12 | + | + | + | – | + | + | – | + | – | + | – | – | + | – | – | – |
| *13 | + | – | – | + | + | + | – | – | – | – | + | + | + | – | – | + |
| 14 | + | + | – | + | + | – | + | + | – | – | + | – | – | + | – | – |
| 15 | + | – | + | + | + | – | – | – | + | + | + | – | – | – | + | – |
| *16 | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + |
The full factorial requires 16 runs if it is only replicated one time. It allows you to estimate the effects of the 4 factors, the 6 two-factor interactions, the 4 three-factor interactions and the 1 four-factor interaction.
Suppose we decided to make only the eight runs marked with a * in the above table. Reorganizing the eight runs gives:
Table 5: Half of a 24 Factorial Design Table
| Run | A | B | C | D = ABC |
|---|---|---|---|---|
| 1 | – | – | – | – |
| 10 | + | – | – | + |
| 11 | – | + | – | + |
| 4 | + | + | – | – |
| 13 | – | – | + | + |
| 6 | + | – | + | – |
| 7 | – | + | + | – |
| 16 | + | + | + | + |
Note that the first three columns of this design are the levels of the factors for a 23 full factorial. Also note that the column for factor D has the same signs as the column for the three-factor interaction, ABC. This eight-run design is called a half fraction or a half replicate of a 24 full factorial design. It is often designated as a 24-1 fractional factorial design since (1/2)24 = 2-124 = 24-1. This tells us that the design is for four factors, each at two-levels, but that only 24-1 = 23 = 8 runs are used.
How did we come up with this design? A full 23 design was written for the variables A, B and C. The column of signs for the ABC interaction was used to define the levels of factor D as is shown in the table below.
Table 6: Building a 24-1 Fractional Factorial Design Table
| Run | A | B | AB | C | AC | BC | D |
|---|---|---|---|---|---|---|---|
| 1 | – | – | + | – | + | + | – |
| 2 | + | – | – | – | – | + | + |
| 3 | – | + | – | – | + | – | + |
| 4 | + | + | + | – | – | – | – |
| 5 | – | – | + | + | – | – | + |
| 6 | + | – | – | + | + | – | – |
| 7 | – | + | – | + | – | + | – |
| 8 | + | + | + | + | + | + | + |
By running this design, we can obtain the main effects of the four factors with just eight runs. It appears that we have gained something for nothing. The eight-run half fraction will give us the 4 main effects and 3 two-factor interactions. But we do lose some information.
The full 24 factorial design gave us more information – the 4 factors, the 6 two-factor interactions, the 4 three-factor interactions and the 1 four-factor interaction. What happened to the other 3 two-factor interactions, the 4 three-factor interactions and the 1 four-factor interaction? Well, they are “confounded.”
Let’s estimate the three-factor interaction ABD. To determine the levels of ABD for each run, you multiply the levels of A times B times D. For example, for run 1, factors A, B and D are all at their low or -1 level. Thus, for run 1:
Level of ABD = (-1) (-1) (-1) = -1
The first sign in column ABD is a minus sign. The other entries in the column are determined in the same manner. The three-factor interaction ABD is given by in the table below.
Table 7: ABD Confounding Example
| Run | ABD |
|---|---|
| 1 | – |
| 2 | – |
| 3 | – |
| 4 | – |
| 5 | + |
| 6 | + |
| 7 | + |
| 8 | + |
Look at the design table above. The levels of ABD match the levels of factor C. We say these two effects are confounded. We know the effect but don’t know how much is due to factor C and how much is due to the three-factor interaction ABD. How can we easily determine which other factors are confounded without having to generate columns of pluses and minuses?
The 24-1 design was constructed by setting D = ABC. This is called the generator of the design. This is not an equality. It means simply that the effect of D is confounded with the interaction ABC. In many books, it will be written as D + ABC.
Suppose we multiply each side of the generator by D.
D * D = ABC * D
D2 = ABCD
We will define any effect times itself to be equal to 1 (e.g. D2 = 1). There is no mathematical meaning to this. It helps us to generate the confounding patterns in a design. Thus 1 = ABCD. This is called the defining relationship of the design. It is the key to the confounding patterns.
For example:
1 = ABCD
C * 1 = ABCD * C
C = ABC2D
C = ABD (as shown already)
The confounding pattern for all factors is then easily found.
1 = ABCD
A = BCD
B = ACD
C = ABD
D = ABC
AB = CD
AC = BD
AD = BC
In this 24-1 design, the main effects are confounded with the three factor interactions, while the two factor interactions are confounded with other two factor interactions. The design table, with the confounding, is given below.
Table 8: 24-1 Fractional Factorial Design Table with Confounding
| ABCD | BCD | ACD | CD | ABD | BD | AD | ABC | |
|---|---|---|---|---|---|---|---|---|
| = | = | = | = | = | = | = | = | |
| Run | Mean | A | B | AB | C | AC | BC | D |
| 1 | + | – | – | + | – | + | + | – |
| 2 | + | + | – | – | – | – | + | + |
| 3 | + | – | + | – | – | + | – | + |
| 4 | + | + | + | + | – | – | – | – |
| 5 | + | – | – | + | + | – | – | + |
| 6 | + | + | – | – | + | + | – | – |
| 7 | + | – | + | – | + | – | + | – |
| 8 | + | + | + | + | + | + | + | + |
If three and four factor interactions are assumed to be zero, this design gives estimates of the average and the four main effects. The two factor interactions are still confounded with other two factor interactions, however. The defining relationship 1 = ABCD gave the runs with asterisks in the 24 full factorial design shown in Table 4. The complementary half fraction is given by 1 = -ABCD. This gives the runs not asterisked in Table 4. Either confounding scheme can be used.
Of course, software today will generate all these confounding schemes for you, but it is helpful to have a basic understanding of how the design tables are generated and what effects and interactions are confounded.
Design Resolution
The 24-1 fractional factorial design is called a resolution IV design. The main effects are confounded with third order interactions, and two order interactions are confounded with other two order interactions. In general, a design of resolution R is one in which no p-factor effect is confounded with any other effect less than R-p factors.
For example:
- R=III does not confound main effects with one another but does confound main effects with two order interactions.
- R=IV does not confound main effects and two order interactions but does confound two order interactions with other two order interactions.
- R= V does not confound main effects and two order interactions but does confound two order interactions with third order interactions.
In general, the resolution of a two-level factorial design is the length of the shortest word in the defining relationship. For example, in the defining relationship 1 = ABCD, the term ABCD is called a word. Its length is four, so the design has a resolution of IV.
In our next publication, we will look at a couple of examples of fractional factorial designs including how to analyze and interpret the results.
Summary
This publication has introduced how fractional factorial designs are setup. The publication started with a review of experimental design terminology and full factorial designs. Fractional factorial designs are beneficial because higher-order interactions (three factor and above) are often insignificant. This allows you to obtain the effect of factors and two-factor interactions with fewer runs.