Process Capability and Non-Normal Data

July 2014

This month’s publication takes a look at process capability calculations and the impact non-normal data has on the results. The most common method of expressing process capability involves calculating a Cpk value, i.e., a process has a Cpk = 1.54. In our April publication, we explained why a Cpk value by itself is not sufficient for defining process capability – and that is if your data are somewhat normally distributed. If your data are not normally distributed, then forget it. Cpk, applied to the raw data, is pretty much worthless as a measure of process capability.

Remember, not all data are normally distributed. There are many naturally occurring distributions. For example, the exponential distribution is often used to describe the time it takes to answer a telephone inquiry, how long a customer has to wait in line to be served, or the time to failure for a component with a constant failure rate. These types of data have many short time periods with occasional long time periods. These data are not described by a normal distribution.

So, how can you handle these types of data when it comes to process capability? This publication examines how this is done using the exponential distribution as an example. In this issue:

• Exponential Example Data
• The Wrong Approach: Cpk
• The Correct Approach: Non-Normal Ppk
• Previous Process Capability Publications
• Summary
• Quick Links

Exponential Example Data

We will use the same data set that we used last month to take a look at the impact of non-normal data on control charts. Our data set consists of 100 random numbers that were generated for an exponential distribution with a scale = 1.5. The scale is what determines the shape of the exponential distribution. Suppose these data describe how long it takes for a customer to be greeted by a salesperson in a store. Usually a customer is greeted very quickly. Sometimes it is crowded in the store and it takes longer. The data are shown in Table 1.

Table 1: Exponential Data

Management has set the goal that every customer must be greeted by a salesperson within six minutes of when they enter the store. This is the upper specification limit (USL) for our process. There is no lower specification limit (LSL). You have collected the data in Table 1 and now want to determine if the process is capable of meeting the specification set by management.

To perform a Cpk calculation, two things need to be true. First, the process must be in statistical control. Second, the data must be somewhat normally distributed. Last month’s publication examined these data as a control chart. The process is in statistical control. So, the first assumption is satisfied.

Are these data normally distributed? Last month’s publication also showed the histogram and normal probability plot for these data. These two techniques demonstrated quite clearly that the data are not normally distributed. So, the second assumption of normality is not satisfied. But suppose you don’t take the time to find that out – that you just merely ignore the assumptions used for determining process capability and move forward with calculating Cpk based on the data in Table 1.

The Wrong Approach: Cpk

One thing is for sure – calculating Cpk from non-normal data is just plain wrong. Yet, it is amazing how often people do that. Our USL is 6 minutes. We have our software program or Excel template on process capability. We plug in our numbers and get our Cpk. It equals 1.1. It is greater than 1 so essentially nothing is out of specification! We are happy! (Don’t look at the data in Table 1. A couple points are above the USL. Just ignore that little fact.)

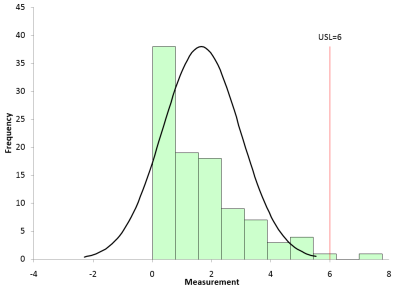
Again, a number by itself means nothing. You need to look at the relationship between the histogram, the specifications and your assumed distribution. This can be done examining the process capability chart shown in Figure 1.

Figure 1: Process Capability Chart – Normal Distribution

This chart shows the histogram of the raw data, the normal distribution based on the average and standard deviation of the raw data, and the specification limits (only a USL in this case). What do you notice about this chart? A few things stand out.

• The normal distribution does not appear to fit the histogram, so a basic assumption of normality for calculating the Cpk value is not valid.
• The normal distribution has values below zero – clearly not the case for waiting time. No matter how quickly you greet customers, the time will not be a negative number.
• The tail of the normal distribution approaches zero at time a little less than 6 implying there are no values about that.
• There are some points (2 to be precise) above the USL.

Some of the calculated statistics from this analysis are given below. These calculations assume that the data are normally distributed.

• Within Capabilities:
  • Cp=N/A
  • Cpk=1.1
  • Cpu=1.1 (0.05%)
  • Cpl=N/A (0%)
  • Est. Sigma (σ) =1.316
  • PPM>USL=485.35
  • PPM<LSL=0
  • Total PPM=485.35
• Overall Capabilities:
  • Pp=N/A
  • Ppk=0.94
  • Ppu=0.94 (0.24%)
  • Ppl=N/A (0%)
  • Sigma (s) = 1.545
  • PPM>USL=2466.74
  • PPM<LSL=0
  • Total PPM=2466.74
  • Average (X)= 1.658

The within capabilities (Cpk calculations) are based on the estimated standard deviation from the average range (σ), while the overall capabilities are based on the calculated standard deviation (s). There are no values for Cp, Cpl, etc. since there is no LSL.

The equations for Cp, Cpk, Cpu, and Cpl are given below. The equations for Pp, Ppk, Ppu, and Ppl are identical except that the estimated standard deviation, σ, is replaced by the calculated standard deviation, s.

Cp=(USL-LSL)/6σ

Cpu=(USL-X)/3σ

Cpl=(X-LSL)/3σ

Cpk is the minimum of Cpu and Cpl. The calculations don’t care if the data are normally distributed or not. Plug in the numbers and you get results for each of the values. But these calculations don’t mean much if the data are not normally distributed. For example consider the value of Cpu above. Cpu = 1.1 and the theoretical % above the USL is 0.05%. But there are 2 points out of 100 that are above the USL. This is 2% – considerably different than 0.05%. This is a result of the assumptions (a normal distribution in this case) not being valid.

So, how do you handle non-normal data and process capability?

The Correct Approach: Non-Normal Ppk

If you have non-normal data, you have two options. First, you can transform the data (using something like the Box-Cox or Johnson transformations), if possible, so that the transformed data follows a normal distribution. Then perform the Cpk calculations. The problem with this approach is that the original data format is lost by the transformation. A waiting time of 4.5 is no longer 4.5, but a transformed number. The transformed data no longer reflect the times to greet a customer. This confuses things to someone else looking at the results.

Second, you can select a distribution that fits your situation, both theoretically and based on the raw data. This is the best approach because it maintains the data format and helps you with your understanding of your process. This is what we will cover below. With this approach, Cpk disappears from the picture. It is not calculated at all since the equations that produce Cpk depend on the assumption that you have a normal distribution.

The first step is to determine what distribution your data follows. This is an important step. You can easily put your data into a software package that will test many different distributions to find out which distribution fits your data best. But you should have a reason for using a certain distribution – it must make sense in terms of your process. For example, with the waiting time data in Table 1, it makes sense that it follows an exponential distribution. Will a three-parameter gamma distribution fit your data better? Maybe based on the numbers, but not on the process.

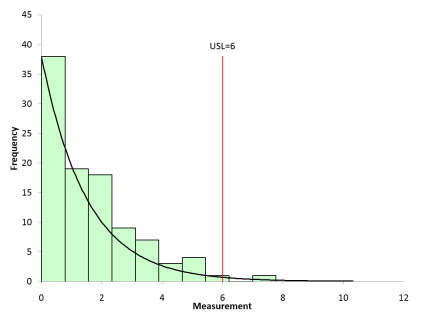
Once you know your distribution, you can generate a process capability chart based on the non-normal data. This chart is shown in Figure 2.

Figure 2: Process Capability Chart – Exponential Distribution

This process capability chart has the exponential distribution (with scale = 1.5) superimposed on the histogram. It is easy to see that the distribution fits the histogram well. Also note that the exponential distribution has a very long tail to the left, approaching zero at a waiting time above 10 – completely different than the normal distribution in Figure 1.

The calculated statistics with this chart are shown below.

• Overall Capabilities:
  • Pp=N/A
  • Ppk=0.56
  • Ppu=0.56 (1.83%)
  • Ppl=N/A
  • PPM>USL=18315.64
  • PPM<LSL=N/A
  • Total PPM=18315.64

Note that value for Ppk (0.56) is considerably less than when the Cpk calculation was done, which gave a Ppk = 0.94. In addition, note that the estimated % above the USL is 1.83 for the non-normal process capability chart – much more in line with the actual results. This is the preferred approach for non-normal process capability calculations. You still interpret the numbers as before. Values of Ppk greater than 1.0 are desirable – the higher the better.

The formulas for Ppk look different than for the normal distribution. The values depend on the type of the distribution you are using. The formulas are given below.

Pp=(USL-LSL)/(X_.99865-X_.00135 )

where USL = upper specification limit, LSL = lower specification limits, X_.99865 = 99.865th percentile of the exponential distribution, and X_.00135 = 0.135th percentile of the exponential distribution (or your specified distribution).

Ppl=(X_.5-LSL)/(X_.5-X_.00135)

where X_.5 = 50th percentile of the exponential distribution.

Ppu=(USL-X_.5)/(X_{_.99865}-X_.5)

Ppk is the minimum of Ppu and Ppl. The percentiles above match the percentiles of a normal distribution for ± three sigma – the distance from the average to the average ± three sigma.

Previous Process Capability Publications

If you are new to process capability, please see some of our previous publications on process capability. All these publications assume that the data follow a normal distribution.

• Process Capability – Part 1 (October 2004)
• Process Capability – Part 2 (November 2004)
• Process Capability – Part 3 (December 2004)
• Cpk Improvement Methodology (February 2012)
• An Interactive Look at Process Capability (March 2014)
• Cpk Alone is Not Sufficient (April 2014)
• Cpk vs Ppk: Who Wins (May 2014)

You can access these publications here.

Summary

This publication examine how non-normal data impacts process capability calculations and results. With non-normal data, it is wrong to calculate a Cpk based on the raw data. A better approach is to determine what distribution best fits your process and data and then use the non-normal Ppk approach. The equations for Ppk are different for non-normal data than for normally distributed data.