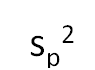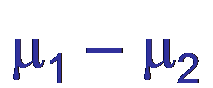February 2007
In this issue:
In August 2006 we examined how to compare two processes. Sometimes you will need to compare more than two processes. For example, you might be comparing the products produced by three different shifts or from three sister plants. The question is, “Are the processes making the same product?” This month’s newsletter demonstrates how to compare the products from multiple processes when there are not sufficient data to use control charts.
Multiple Processes
The calculated standard deviation (the variation) will also be different for the three reactors. Again, are these differences significant? In this newsletter, you will see how to compare the variances in multiple processes to see if they are the same. And if the variance is the same, you can construct multiple confidence intervals for the difference in paired sets of averages. These confidence intervals will tell you if there are any significant differences in the averages.
The method described below (called Bonferroni’s method) is one method of examining multiple processes. Bonferroni’s method develops multiple confidence intervals for the differences in averages. Every possible combination of a pair of processes is examined. If the confidence interval contains zero, there is no difference in the averages of the two processes. If the interval does not contain zero, there is evidence that the two processes are operating at different averages. Differences in variances are checked through the use of a standard deviation (s) control chart.
This technique represents a snapshot in time for the two processes. You cannot be sure of obtaining similar results in the future unless the processes are in statistical control.
Suppose there are four different furnaces producing ethylene. The % ethylene is an important parameter for each furnace. The question is: Is the % ethylene content the same for each furnace?
To determine this, we take seven samples from each furnace. We will use “n” to denote the number of the samples. So, in this case, n = 7. We will use “k” to denote the number of processes. Since we have four furnaces, k = 4.
The raw data for % ethylene from each furnace is shown below.
Furnace 1: 67, 67, 64, 65, 64, 65, 67
Furnace 2: 64, 65, 67, 64, 65, 68, 64
Furnace 3: 68, 65, 67, 64, 67, 65, 65
Furnace 4: 69, 72, 70, 68, 67, 68, 70
Some sample statistics can be calculated for each process. We will use X for the average of the sample results, sigma for the standard deviation of the samples and Var for the variance of the samples. For the four furnaces:
Furnace 1: X =65.57, Sigma = 1.397, Var = 1.952
Furnace 2: X = 65.29, Sigma = 1.604, Var = 2.571
Furnace 3: X = 65.86, Sigma = 1.464, Var = 2.143
Furnace 4: X =69.14, Sigma = 1.676, Var = 2.810
We will use these calculated statistics to compare the four furnaces. We start first with the question:
Is the variation the same for all the processes?
Comparing the Variation

The first step is to find the average standard deviation (s). This is simply done by adding up the standard deviation for each furnace and dividing by the number of furnaces. Thus,
s = (1.397 +1.604+1.464+1.676)/4=6.141/4 =1.535
The next step is to calculate the control limits for the s chart. The upper control limit (UCL) and the lower control (LCL) are given by the equations below:
UCL = B4s
LCL = B3s
B4 and B3 are control chart constants that depend on the subgroup size (n). As long as none of the standard deviations are above the UCL or below the LCL, it is assumed that the processes operate with the same variation. If this is not true, Bonferroni’s method cannot be used.
For a subgroup size of 7, B4 = 1.882 and B3 = 0.118. The control limits are then:
UCL = B4s = 1.882(1.535) = 2.89
LCL = B3s= 0.118(1.535) = 0.18
Since none of the standard deviations for the furnaces are above the UCL or below the LCL, we conclude that the variance of the four furnaces is the same.
Once it has been determined that the variation is consistent between the processes, the confidence intervals for the difference between any set of two averages can be constructed. The first step in doing this is to estimate the variance of the four processes using the sample results. The procedure for doing this is shown in the next section.
Pooled Variance
The next step is to estimate the pooled variance. There are four estimates of the variance from the sample variances. These are pooled to get a single estimate of the variance. The pooled variance is given by:
sp2 = [(n1-1) s12 + (n2-1)s22 + .. + (nk-1) sk2]/[n1 + n2 + .. + nk – k]
The pooled variance is just a weighted average of the sample variances based on degrees of freedom for each sample. The square root of the pooled variance is a measure of the part-to-part variation or the process standard deviation using information from the four samples.
The pooled variance for this example is then given by:
sp2 = [6(1.952)+6(2.571) +6(2.143)+6(2.810)]/ [7+7+7+7-4] = 2.369
The pooled variance is used to help estimate the standard deviation, sdiff, which estimates the variation of differences in two sample averages for process i and process j.
sdiff =SQRT [sp2((1/ni)+ (1/nj))]
If the number of observations (n) from each process is the same, the value of this standard deviation will be the same for all combinations of process i and process j. If not, this value will change when n changes and must be recalculated. Calculations are made simpler by keeping n constant.
For the four furnace problem, the standard deviation is:
sdiff =SQRT [sp2((1/ni)+ (1/nj))] = sqrt [2.369 ((1/7)+(1/7))] = 0.822
This standard deviation will now be used to set up the confidence intervals to determine if there are any differences in the process averages.
Comparing the Averages
A confidence interval is developed for each possible pair of processes. There are a total of R = k(k-1)/2 confidence intervals. Thus for the furnace example, there are R = 4(4-1)/2 = 6 confidence intervals to be constructed.
Let μ represent the true (unknown) average of a process. The 100(1 – α)% confidence interval for μi– μjis given by
Xi – Xj ± tsdiff
where t is the value for the t distribution The value of t can be found in the t tables of many statistics books. It is also available in Microsoft Excel using the TINV function.
The value of t is determined by the confidence coefficient (1 -α) and the degrees of freedom. The degrees of freedom are those used in determining the pooled variance. Thus, the degrees of freedom are:
df = n1 + n2 +…+ nk – k
For the furnace example, the degrees of freedom are:
df = 7 + 7 + 7 + 7 -4 = 24
To determine t, we also need the confidence coefficient. If we want an overall confidence of 95%, we will need to use a confidence coefficient of 1 -(α/R) for the t value. Thus, the more processes we have, the smaller the confidence coefficient for each process.
For the four furnace example and an overall confidence of 95%, the confidence coefficient for t is 1 – (0.05/6) = 0.992. This gives anαof 0.008 for each confidence interval.
The value of t for 24 degrees of freedom and 99.2% confidence is 2.892.
The six intervals can now be constructed. Each interval will have the following format:
Xi – Xj ± tsdiff
Xi – Xj ± 2.892(0.822)
Xi – Xj ± 2.38
Using this general format, the intervals become:
X1 – X2 ± 2.38 = 65.6 – 65.3 ± 2.38 = 0.3 ± 2.38 or [-2.08 to 2.68]
X1 – X3 ± 2.38 = 65.6 – 65.9 ± 2.38 = -0.3 ± 2.38 or [-2.68 to 2.08]
X1 – X4 ± 2.3 = 65.6 – 69.1 ± 2.38 = -3.5 ± 2.38 or [-5.88 to -1.12]
X2 – X3 ± 2.38 = 65.3 – 65.9 ± 2.38 = -0.6 ± 2.38 or [-2.98 to 1.78]
X2 – X4 ± 2.38 = 65.3 – 69.1 ± 2.38 = -3.8 ± 2.38 or [-6.18 to -1.42]
X3 – X4± 2.38 = 65.9 – 69.1 ± 2.38 = -3.2 ± 2.38 or [-5.58 to -0.82]
If the confidence interval does not contain zero, it is concluded that the two processes are operating at different averages. If the confidence interval does contain zero, you conclude that there is no evidence that the two processes are operating at different averages. They appear to have the same average.
By examining the intervals above, it can be concluded that furnaces 1, 2 and 3 operate at the same average. When comparing any combination of these, the confidence interval always contains 0. It appears that furnace 4 operates at an average different than the other three furnaces. Any interval containing furnace 4 does not contain 0.
This method provides a way of comparing the averages and variation in multiple processes. Please remember that, if the processes are not in statistical control, you may not get similar results when the test is repeated.
Summary
This newsletter showed how to compare multiple processes. Samples are taken from each process. The average and standard deviation of each process is calculated. A “s” control chart is used to determine if the variance is the same for each process. If so, the Bonferroni method cannot be used. If the variances are the same, each pair of averages are compared. The t distribution is used to develop a confidence interval around the difference in each pair of averages. If the interval contains zero, we conclude that those two processes represented by the pair of averages do not have significantly different averages. If the interval does not include zero, we conclude that those two processes have different averages.