SPC and Rational Subgrouping

February 2013

This is the second part of our rational subgrouping newsletter.  Rational subgrouping is a very important concept in Statistical Process Control (SPC), but it is often forgotten.  Far too often, people do not give enough (or any) thought about how to subgroup their data when constructing an  X-R control chart or any other control chart that involves putting the data into subgroups.  One needs to remember that control charts are really a study of the variation in your process.  And the variation displayed on the control chart depends on how you subgroup your data – which may or may not be the variation you would like to study.

In our last newsletter, we used the sport of golf to help us explore rational subgrouping.  In this newsletter, we will take a look at two major “rules” for rational subgrouping.    We will use a process that involves four machines making the same part to help us understand how subgrouping impacts what a control chart is monitoring.    We will look at three different subgrouping plans and, then, we  will figure out which subgrouping plan is best by following some of our “rules” for subgrouping.

In this Issue:

• The Four Machines
• Sampling and Measuring the Process – Preserving the Information
• Rational Subgrouping
• Subgrouping Variation with the Machines
• Summary
• Video: Rational Subgrouping
• Quick Links

The Four Machines

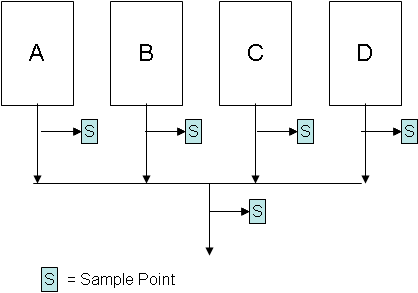
Our process is shown in Figure 1.  There are four machines that make the same part.  The sampling points in the process are also shown in the figure.   A major customer is interested in our monitoring a certain quality characteristic (X).

Figure 1: Four Machine Process

We want to use an X-R control chart to monitor our process.  Three different subgrouping plans using a subgroup size of four are being discussed.  The three plans are described below.

• Plan A:  Select the first subgroup to consist of four samples from machine A, the second subgroup to consist of four samples from machine B, the third subgroup to consist of four samples from machine C and the fourth subgroup to consist of four samples from machine D. Repeat this sequence over time.
• Plan B:  Select one sample from each machine to form the subgroup of four each time.
• Plan C:  Select each subgroup to consist of four samples from the blended stream.

Take a look at these three plans.  Can you answer the following questions?

1. Which subgrouping plan do you think is best?
2. Why?
3. What variation would be monitored on the X chart and the R chart for each plan?

The third question is really the key.  You want to subgroup data to explore the variation you are interested in.  We will take a look at these three plans in more detail, starting with how we sample our process.

Sampling and Measuring the Process – Preserving the Information

Rational subgrouping starts with how you sample and measure your process.  For any process, you will need to decide the following four items:

1. What will be measured
2. How it will be measured
3. Where it will be measured
4. How often it will be measured

Of course, you need to be concerned with how accurate and precision your measurement process is, but, for this example, we will assume that we have a great measurement system.  We can measure our quality characteristic X without any problems.

Remember that one purpose of control charts is to monitor a process for out of control points.  When a process goes out of control, a special cause of variation is present and you will need to search for what caused this out of control situation.  Thus, it is important that you know when and where the sample was produced.  Without that information, it is impossible to go back and see what happened.

Does this cast any doubt about one of the sampling plans above?  Take a look at Plan C.  We are combining the four streams from each machine and taking a sample from the blended stream.  What happens if one of our subgroups goes out of control?  We don’t know which machine(s) the parts came from because we blended the streams together.  We have lost the production information (which machine at what time) about the parts in those subgroups.  Our data are totally worthless – not only for searching for the reason for the out of control point but also for process improvement efforts.  So, even without any data taken yet, we know that Plan C is probably not going to work for us.

Rational Subgrouping

We introduced rational subgrouping last month using golf as an example.  A pro golfer plays four rounds of golf in a tournament.  This provided us with a rational way of subgrouping the data.  We used those four rounds of golf to form a subgroup. For each subgroup, we calculated the average of the four rounds (the tournament average) and the range for the tournament (the maximum minus the minimum round).  We then used the X chart to monitor the variation in the average tournament score from tournament to tournament.   We used the range chart to monitor the variation within a tournament.  Control charts are about monitoring variation.

Whenever you look at a control chart, the first question you should ask yourself is

What variation is this chart examining?

If you can’t answer this question, then the control chart is nonsense – it will not tell you anything at all.  Throw it out and start over with a discussion of rational subgrouping.  In control chart language:

The X control chart is monitoring the variation in the subgroup averages from subgroup to subgroup.

The R chart is monitoring the variation within the subgroup from subgroup to subgroup.

But these statements by themselves tell you nothing about the process.  You have to be able to restate these in terms of the process being monitored.

The basic idea behind rational subgrouping and forming subgroups is that you want to minimize the opportunity for variation to occur within a subgroup.  This means that you want to form the subgroup under conditions that are essentially the same.  As explain in the last newsletter, the average range is used to set the control limits on the X chart.  So, the within subgroup variation from the range chart is used to determine how much variation there can be between the subgroups on the X chart.

So, the X-R control chart is really answering the following question:

Are there any significant differences in the subgroup averages when we take into account the within subgroup variation?

You want to form the subgroups so the range chart has the greatest potential for being in statistical control.  This lets the X chart do the work in finding special causes of variation.

Here are a few rules to consider for rational subgrouping.

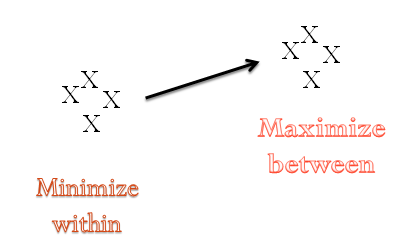
Rule 1: Minimize the variation within a subgroup

Form the subgroups so that there is the minimum chance for variation to occur.  Can you overdo this?  Yes, it is possible.  But most of the time, you should strive to minimize the within subgroup variation.

Rule 2:  Maximize the opportunity for variation to occur between subgroups

This means that if there is an opportunity for two things to be different, be sure to put them in separate subgroups.  Go back to our three subgrouping plans.  We have already ruled out Plan C because it blends the streams thus putting four things that could be different into the same subgroup.  Rule 2 is violated.  What about Plan A and Plan B?   Plan A takes four parts from the same machine and forms a subgroup.  So, each subgroup contains parts from the same machine.  Plan B takes one part from each machine and forms a subgroup.  Note that we are mixing things that could be different – after all they are produced by different machines.  We are violating rule 2 with Plan B.  This seems to leave Plan A as the best subgrouping plan.  It meets the two rules shown in the figure below.

Subgrouping Variation with the Machines

Without looking at any data, we have decided that subgrouping Plan A is the best plan. As stated before, you have to be able to explain the variation that is being monitored on a control chart.  What is the variation being examined by each plan?

Plan A

Plan A involves taking four parts from Machine A and forming a subgroup with those four parts.  The subgroup average and range are calculated.    Then four parts are taken from Machine B and a subgroup is formed.  Again the subgroup average and range are calculated.  This is repeated for Machines C and D.  Then the process starts over.  What variation is being examined on the X and the R charts?

The R chart is monitoring the variation within a machine over time.  The first range value is a measure of the variation within Machine A.  The second range value is the measure of the variation within Machine B.  The range chart is monitoring the within machine variation for the four machines and will answer the following question:

Is the within machine variation the same for all four machines?

i.e., does each machine operate at the same standard deviation?  If the range chart is in control, we will conclude that each machine has the same within variation or operates at the same standard deviation.

The X chart is monitoring the variation in the machine subgroup average over time.  The first X value is the subgroup average for Machine A; the next X value is the subgroup average for Machine B and so on.  So, the X chart is monitoring the variation between machine averages and will answer the following question:

Is the machine average the same for all four machines?

i.e., does each machine operate at the same average?  If the X chart is in control, we will conclude that each of the four machines operates at the same average.

Note that, with this subgrouping plan, it is easy to clearly define what variation each chart is examining.

Plan B

Plan B involves taking a part from each of the machines and forming a subgroup.  The subgroup average and range are calculated.  Then another subgroup is formed by taking one part from each machine.  What variation is being examined on the X and the R charts?

The R chart is monitoring the variation in the range of parts between the four machines.  So, the range chart will answer the following question:

Is the within subgroup variation (the range of parts from the four machines) the same over time?

The X chart is monitoring the average in the four parts from the four machines.  The X chart will answer the following question:

Is the subgroup average (the average of the four machines) the same over time?

Note that the description of what is being monitored in Plan B is a little less precise than in Plan A.  This is because we are mixing our subgroups with parts from different machines.

Plan C

Plan C is simply taking four samples from the combined stream.  In this case, the R chart is monitoring the variation with that subgroup while the X chart is measuring the variation between those subgroups.  Note that not much can be said about what is being monitored.  It is simply the basic description of what the X and R chart do.  If this is all you can say about what is being monitored on a control chart, you do not have rational subgrouping.  All machine information lost because of the blended stream.

Summary

This newsletter has looked at the role rational subgrouping plays in setting up control charts.  You must follow two basic rules when setting up rational subgrouping: minimize the variation within a subgroup and maximize the opportunity for subgroups to be different.  Remember, if you can’t explain what variation is being monitored on a control chart, the control chart is not of any use to you.  And the way you subgroup the data impacts the variation you are examining.

We have two previous newsletters that use data from the three subgrouping plans to show that Plan A provides the most information.    If you are interested, you can see the details here:

• Rational Subgrouping and X-R Charts (May 2005)  – this introduces the machine data, which you can download, and asks questions that you can answer after you make the X-R control charts for each plan.
• Rational Subgrouping and X-R Charts – Part 2 (June 2005) – this newsletters provides the answers and control charts for the machine data.

Video: Rational Subgrouping