September 2005
In this issue:
How do you screen incoming material? Do you try to screen out some or all of the defective items in each incoming lot? Or do you simply send the lot straight to the production line without sorting out the defective items?
Most suppliers do not provide 100% defective-free material. The objective is to pick an incoming sampling plan that provides the minimum average total cost to the company. Quite often, it is either 100% inspection or no inspection. This month’s e- zine examines how this can be done. Also included are instructions for how this can be demonstrated using a deck of cards.
All or None Rule
Under certain conditions, either 100% or no inspection will achieve the minimum total cost for incoming inspection. This is the all-or-none rule that is described in detail in the book Out of the Crisis by Dr. W. Edwards Deming.
There are four assumptions that are required for the analysis.
- We are dealing only with one part
- We will test/inspect the final product before leaving our area
- If the incoming part is defective, the final product will not pass test/inspection; if the incoming part is not defective, the final product will pass test/inspection
- A supply of parts exists to replace defective items
The following definitions are needed:
p = average fraction defective in incoming parts (as determined from a p control chart on the incoming parts)
k1= cost to inspect one part
k2 = cost to repair final product because of defective part (including dismantling, repairing, reassembling and retesting)
k = average cost to find replacement part
k1/ k2 = break even quality
Note: k2 is always greater than k1. Therefore the ratio of the two shall be between 0 and 1.
Under the four conditions listed above, the following is true:
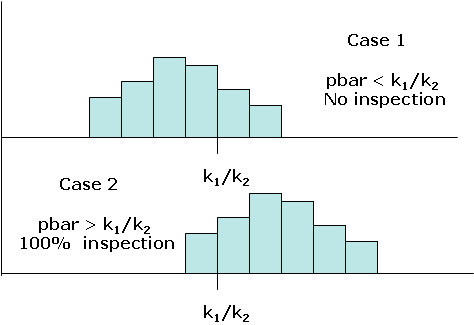
Case 1: If the average fraction defective is less than k1/ k2, the minimum average cost will occur with no inspection.
Case 2: If the average fraction defective is greater than k1/ k2, the minimum average cost will occur with 100% inspection.
These cases are shown in the figure above.
Manufacturing Example
Out of the Crisis contains the following manufacturing example. A company uses integrated circuits to make TVs. The average fraction defective of incoming circuits is pbar = 0.00015. It costs $0.30 to test the integrated circuit, thus k1 = $0.30 The cost to dismantle and repair a TV with a defective integrated circuit is $30.00; thus k2 = 100 k1 = $30.00 Thus,
p = 0.00015 < k1/ k2 = 1/100 = 0.01
This is Case 1. The company should be doing no inspection. Unfortunately, the company was doing 100% inspection and maximizing their costs.
Total cost for 100% inspection is = k1 +k( p )
Total cost for no inspection is = p (k2+k)
Difference (Loss) = k1 +k( p ) – p (k2+k)= k1 – [ p (k2)] = $0.296
Thus, $0.296 is loss on each integrated circuit. The TV uses 60 integrated circuits. Total loss per TV = 60(0.296) = $17.76
Caution about no inspection: No inspection does not mean that you never inspect the incoming material. You inspect enough to know that the supplier’s process is in statistical control. That is a key to applying this approach. The incoming material must be in control with respect to defective items. How often you inspect depends on how often you receive material from the supplier.
Service Example
The following service example is in the book. Work moves from one area to another in a department store. The cost of inspection in a certain area is k1= $0.25 per transaction. The average cost to correct a mistake downstream in the process is k2 = $500.00 The incoming transactions are in statistical control with p = 0.001. Thus:
p = 0.001 > < k1/ k2 = 0.25/500 = 0.0005
Thus, minimum average cost will be obtained with 100% inspection.
Teaching k1/k2
The following is a great way to teach people that this approach works, using playing cards.
Assume the incoming material (15 playing cards) to your department has an average fraction defective, p , equal to 0.25. A playing card is considered to be defective if it is a club. Hearts, diamonds and spades are not defective.
For the fifteen playing cards you select, determine the cost of inspection for both no inspection and 100% inspection.
Group 1
It is known that it costs $1 to inspect each incoming part (k1). It is also known that the cost to repair the problem downstream (k2) is $10
First you are to determine the cost of 100% inspection. Shuffle the deck of cards and deal out fifteen playing cards. In this case there are no k2 costs. It is assumed that defective items never get to the next department. Every item is inspected and costs k1 dollars. Every defective item is replaced by another item produced from the deck of cards. Every replacement produced is inspected and costs an additional k1 dollars. Produce items until all the card are conforming (i.e., hearts, diamonds, or spades). Determine the total cost of inspection.
You are then to determine the cost of no inspection. Shuffle the deck and deal out fifteen playing cards. There are k1 and k2 costs. Each defective item is returned from the next department and costs k2 dollars. Every defective item returned must be replaced by another item produced by the deck of cards. These replacement items must be inspected and each costs k1 dollars. Produce items until all the card are conforming (i.e., hearts, diamonds, or spades). Determine the total cost of inspection.
Group 2
It is known that it costs $2 to inspect each incoming part (k1). It is also known that the cost to repair the problem downstream (k2)is $5
First you are to determine the cost of 100% inspection. Shuffle the deck and deal out fifteen playing cards. In this case there are no k2 costs. It is assumed that defective items never get to the next department. Every item is inspected and costs k1 dollars. Every defective item is replaced by another item produced from the deck of cards. Every replacement produced is inspected and costs an additional k1 dollars. Produce items until all the card are conforming (i.e., hearts, diamonds, or spades). Determine the total cost of inspection.
You are then to determine the cost of no inspection. Shuffle the deck and deal out fifteen playing cards. There are k1 and k2 costs. Each defective items is returned from the next department and costs k2 dollars. Every defective item returned must be replaced by another item produced by the deck of cards. These replacement items must be inspected and each costs k1 dollars. Produce items until all the card are conforming (i.e., hearts, diamonds, or spades). Determine the total cost of inspection.
Summary
This month’s newsletters took a look at an example from Dr. Deming’s book Out of the Crisis. It demonstrated that. under certain conditions, either 100% or no inspection will achieve the minimum total cost for incoming inspection. This is the all-or-none rule. We also introduced a simple method of teaching this concept using playing cards.