December 2022
(Note: all the previous SPC Knowledge Base in the basic statistics category are listed on the right-hand side. Select this link for information on the SPC for Excel software.)

- Determine the relationship between pairs of items/questions.
- Evaluate how consistent the survey or test is.
- Determine whether removing some items/questions improves how consistent the survey or test is.
Scatter plots are used to determine the relationship between each pair of items/questions. A metric called Cronbach’s Alpha is used to evaluate how consistent the survey or test is. And finally, each item/question is omitted from the analysis to see if omitting anything improved how consistent the survey or test is.
In this issue:
- Example
- Item Statistics
- Cronbach’s Alpha
- Omitted Items Statistics
- Scatter Plot Matrices
- Summary
- Quick Links
Please feel free to leave a comment at the bottom of this publication. You can download a pdf copy at this link.
Example
You have a four question survey that measures customer satisfaction. Perhaps the four questions deal with on-time delivery, product performance, after sales follow-up, and ease of payment. You want to know if the questions are reliable – do they all measure the same thing? The questions use the Likert Scale rating of 1 to 5, with 5 representing the highest satisfaction. You would expect a customer who is satisfied to rate the four questions similarly. The results from 25 customers are shown in the table below.
Table 1: Survey Results
| Question 1 | Question 2 | Question 3 | Question 4 |
|---|---|---|---|
| 1 | 1 | 2 | 4 |
| 4 | 3 | 4 | 2 |
| 4 | 2 | 4 | 2 |
| 4 | 5 | 5 | 2 |
| 4 | 3 | 4 | 2 |
| 1 | 2 | 1 | 1 |
| 3 | 3 | 2 | 4 |
| 3 | 4 | 4 | 1 |
| 5 | 5 | 5 | 2 |
| 2 | 1 | 2 | 2 |
| 5 | 4 | 4 | 2 |
| 5 | 4 | 4 | 2 |
| 5 | 5 | 4 | 2 |
| 4 | 5 | 5 | 2 |
| 4 | 5 | 4 | 2 |
| 4 | 4 | 4 | 2 |
| 5 | 4 | 4 | 4 |
| 1 | 1 | 1 | 2 |
| 3 | 3 | 2 | 2 |
| 3 | 3 | 3 | 2 |
| 1 | 1 | 1 | 2 |
| 2 | 2 | 1 | 2 |
| 5 | 5 | 4 | 2 |
| 5 | 5 | 4 | 2 |
| 3 | 3 | 4 | 2 |
These data will be used to perform an item analysis to see if the four questions are measuring the same thing: customer satisfaction. The analysis done below was done with the SPC for Excel software. You can download an Excel workbook containing the results at this link.
Item Statistics
The first step in the analysis is to calculate the basic statistics for each question (or item). The results are shown in Table 2.
Table 2: Item Statistics
| Variable | Count | Mean | StDev | Variance |
|---|---|---|---|---|
| Question 1 | 25 | 3.440 | 1.417 | 2.007 |
| Question 2 | 25 | 3.320 | 1.435 | 2.060 |
| Question 3 | 25 | 3.280 | 1.339 | 1.793 |
| Question 4 | 25 | 2.160 | 0.746 | 0.557 |
| Total | 25 | 12.20 | 3.979 | 15.83 |
The mean is simply the average of each question. You can compare the means to get an idea of the variation in the average results. “StDev” is the standard deviation of each question. The standard deviation and variance are measures of the variation in the results. You can compare these to determine if one question has significantly more or less variation than the others.
The total row uses the total for each survey. For example, the total for the first row in Table 1 is 1+1+2+4 = 8. This is the total for survey 1. The total mean is the average of the totals for each survey and the standard deviation is the standard deviation of the totals for each survey.
The totals and other statistics are used in the calculations below.
Cronbach’s Alpha
A metric called Cronbach’s Alpha is used to measure how consistent the questions are. It is used to determine whether the questions consistently measure the same thing (in this case, customer satisfaction). Cronbach’s Alpha can vary from 0 to 1. Higher values imply more agreement between the questions.
Cronbach’s alpha is calculated using:
where st2 is the sum of the variances, si2 is each individual question variance and k is the number of items in the survey (k = 4 in this example). Cronbach’s Alpha for this example is:
How do you interpret the numeric value of Cronbach’s Alpha? If the numeric value is “large”, then it says that each customer’s response was consistent across all the questions. In our example, if customer 1 is a satisfied customer and rates Question 1 high, they are also likely to provide high responses to the other 3 questions. If Cronbach’s Alpha = 1, there is perfect correlation. Each response is the same for each question.
If the numeric value of Cronbach’s Alpha is small, the questions are not consistent. That is, if a customer rates question 1 high, it does not mean that the customer will response similarly for the other questions. If Cronbach’s Alpha = 0, then there is no correlation between the questions. One response for one question provides no information about the other responses to the questions.
The value of Cronbach’s Alpha will not be 0 or 1 because there is almost always variation in the results. The following is usually used for Cronbach’s Alpha:
- If Cronbach’s Alpha is greater than 0.7, you have evidence to indicate that the questions measure the same characteristic.
- If Cronbach’s Alpha is less than 0.7, the questions may not measure the same characteristic.
In our example, Cronbach’s Alpha = 0.793. This would indicate that the four questions measure the same characteristic, customer satisfaction. However, there is more to look at with the Item Analysis just to be sure.
Please note that this calculation does assume that all questions measure the same thing and use the same scale. The scale in this example is 1 to 5 but you can use continuous or binary data as well.
Omitted Item Statistics
This part of the item analysis involves removing each question and rerunning the item statistics and calculating Cronbach’s Alpha. This will determine if removing a question significantly improves the consistency of the survey. The results are shown in Table 3.
Table 3: Omitted Item Statistics
| Omitted Variable | Adj Total Mean | Adj Total StDev | Adj Total Var | Item Adj Total Corr | Squared Multiple Corr | Cronbach’s Alpha |
|---|---|---|---|---|---|---|
| Question 1 | 8.760 | 2.666 | 7.107 | 0.890 | 0.812 | 0.569 |
| Question 2 | 8.880 | 2.728 | 7.443 | 0.808 | 0.765 | 0.622 |
| Question 3 | 8.920 | 2.798 | 7.827 | 0.829 | 0.764 | 0.614 |
| Question 4 | 10.04 | 3.963 | 15.71 | -0.0727 | 0.0776 | 0.940 |
The first column in Table 3 is the omitted question. The rest of that line are the results without that question in the data. The columns are:
- Adj. Total Mean: this is the sum of the question means omitting the omitted question. You use this to see how the total mean changes as questions are omitted. Look at Questions 1 to 3. They have similar means. So, omitting Questions 1 to 3 does not change the results significantly. But what happens when Question 4 is omitted? The total mean changes quite a bit.
- Adj. Total StDev: this is the standard deviation of the total scores after omitting a question. You use this to compare the variation as questions are omitted. Omitting Question 4 causes an increase in the standard deviation.
- Adj. Total Var: this is the variance of the total scores after omitting a question. You use this to compare the variances as questions are omitted. Omitting Question 4 causes an increase in the variance.
- Item Adj. Total Corr: this is the correlation between the scores of the omitted question and the total scores for the remaining questions. If this value is close to 1, there is no impact of omitting the question. If the value is not close to 1, there may be an impact of omitting the question. Again, question 4 is suspect.
- Squared Multiple Corr: this is the R2 value when a regression is run between the omitted question (as the y value) and the remaining questions. This is used the same way as the Item Adjusted Total Correlation. Omitting Question 4 shows a big difference as well.
- Cronbach’s Alpha: this is the metric calculated above but with a slightly different equation to account for omitting a question:
where st2j is the sample variance of the total after omitting the jth question. The Cronbach’s Alpha when Questions 1 to 3 are omitted are very similar. It is much higher when Question 4 is omitted.
In summary, look at Table 3. Look at the results when Questions 1 to 3 are omitted. They are very similar. But what happens when Question 4 is omitted? The results in Table 3 are quite different. If an omitted question has a significantly higher Cronbach’s Alpha along with a significantly lower Item Adjusted Total Correlation value, and a significantly lower Squared Multiple Correlation value, then that question should probably be removed from the analysis.
In this example, it appears that Question 4 should be removed from the analysis. Note that this is true even though Cronbach’s Alpha was greater than 0.70. You cannot rely simply on the value of Cronbach’s Alpha.
Scatter Plot Matrices
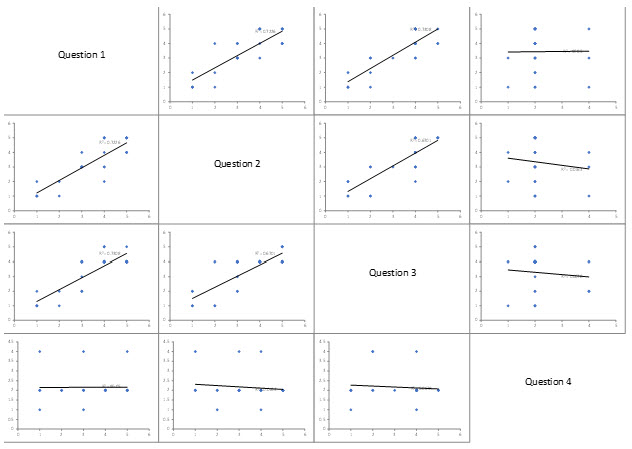
Scatter plots are used to visually see the relationship between pairs of questions. The scatter plots for these four questions are shown in Figure 1.
Figure 1: Item Analysis Scatter Plots
You can download an Excel workbook containing the Item Analysis results at this link to see the scatter plots better. A scatter plot simply plots each pair of questions against each other. If the slopes are fairly steep, there is probably a significant correlation between the two questions. You can see from the plot if the slope is positive or negative. The scatter plot matrix in Figure 1 shows a positive correlation between Questions 1 to 3. However, the slopes for the scatter plots involving Question 4 are almost horizontal lines. This implies that Question 4 is not measuring the same thing as Questions 1 to 3.
Summary
This publication introduced the Item Analysis technique that is used to analyze how consistent surveys or tests are. The technique looks at three things:
- Determining the relationship between pairs of questions on the survey using scatter plots.
- Evaluating how consistent the survey is using the questions statistics to calculate Cronbach’s Alpha metric; the higher the metric the more consistent the questions are.
- Determining whether removing some questions improves how consistent the survey is by calculating statistics including Cronbach’s Alpha to see if any of the statistics change significantly.
You need all three things to get a good picture of the consistency of the survey. A four question survey was used as an example. It was found that one question should be removed from the example survey.
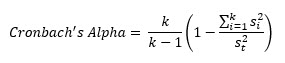
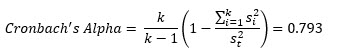

HelloGood article, very practical and relevant. Thank you for sharingJust one question from me, how did you get: 3.97911212877111 – sum of Standard DeviationsRegards
Hello Erick,
Thanks for the comments. I did a very poor job of explaining that in the newsletter. I rewrote it make it clearer;
The total row uses the total for each survey. For example, the total for the first row in Table 1 is 1+1+2+4 = 8. This is the total for survey 1. The total mean is the average of the totals for each survey and the standard deviation is the standard deviation of the totals for each survey.”
Let me know if you have any other questions.
All clear now Bill, thank you so much