August 2006
In this issue:
- Two Processes
- Comparing the Variances
- Estimating the Variance
- Difference in Two Averages
- Example
- Summary
- Quick Links
Sometimes you will need to compare two processes. For example, you might be comparing the products from two different suppliers or from two sister plants. You might be comparing two ways of processing invoices. The question is, “Are the two processes making the same product?” This month’s newsletter demonstrates how to compare the products from two different processes when there is no sufficient data to use control charts.
Two Processes

Suppose there are two processes (such as two different reactors) making the same product. Suppose n1 samples are taken from process 1 and n2 samples are taken from process 2. Some sample statistics can be calculated.
Process 1:
- Sample size: n1
- Sample average: X1
- Sample variance: s12
Process 2:
- Sample size: n2
- Sample average: X2
- Sample variance: s22
The procedure for comparing two processes is given below. This technique represents a snapshot in time for the two processes. You cannot be sure of obtaining similar results in the future unless the processes are in statistical control.
Comparing the Variances

To calculate the F value based on sample results, the larger sample variance is divided by the smaller sample variance.
F = Larger s2/Smaller s2
To determine if there is a difference in the variances of the two processes, this calculated value of F is compared to a critical F value from the tables for the F distribution. The table values of F depend on two degrees of freedom. v1is the degrees of freedom in the variance in the numerator (n1– 1). v2is the degrees of freedom in the variance in the denominator (n2– 1). The other item that the table values of F depend upon is the confidence coefficient (α). A value of α = 0.05 is typical.
Many statistical books contains the F tables. You can also determine the F value using Microsoft Excel’s function FINV. This gives the critical value of F for a given confidence coefficient and the two degrees of freedom.
If the calculated value of F is larger than the table (critical) value, it is concluded that there is a difference in the two variances. If the calculated value is less than the table value, it is concluded that there are no differences in the two variances.
Once it has been determined that the variation is consistent between the two processes, the confidence interval for the difference between the two averages can be constructed.
Estimating the Variance
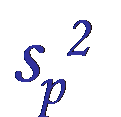
sp2 = [(n1 – 1)s12 + (n2 – 1)s22]/(n1 + n2 – 2)
The pooled variance is just a weighted average of the sample variances based on degrees of freedom for each sample. The square root of the pooled variance is a measure of the part-to-part variation or the process standard deviation using information from both samples.
Difference in Two Averages
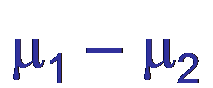
sdiff =SQRT [sp2((1/n1)+ (1/n2))]
This standard deviation is then used to construct a confidence interval around the difference in the two averages.
Let μ = present the true (unknown) average of a process. The 100(1 – α)% confidence interval for μ1– μ2is given by
X1 – X2 ± tsdiff
where t is the value for the t distribution corresponding to n1 + n2 – 2 degrees of freedom. The value of t can be found in the t tables of many statistics books. It is also available in Microsoft Excel using the TINV function.
If the confidence interval does not contain zero, it is concluded that the two processes are operating at different averages.
If the confidence interval does contain zero, you conclude that there is no evidence that the two processes are operating at different averages. They appear to have the same average.
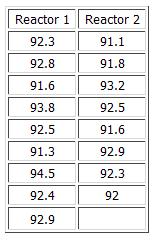
Example
In a plant, two different reactors are making the same product. The question was asked if the reactors produce the same yield. The data below were collected. Is there a difference in the yield from the two reactors?
The first step is to calculate the average and variance for each of the reactors. The variance is the square of the standard deviation. The results are:
Reactor 1:
- Average = 92.68
- Variance = 0.994
- Observations = 9
Reactor 2:
- Average = 92.18
- Variance = 0.480
- Observations = 8
The next step is to calculate the F value by dividing the larger variance (Reactor 1) by the smaller variance (Reactor 2).
F = Larger s2/Smaller s2 = 0.994/0.480 = 2.07
The next step is to compare the calculated value of F with the critical value of F. There are 8 degrees of freedom in the numerator and 7 degrees of freedom in the denominator.
For α =0.05, the critical value of F is 3.73 (using the FINV function in Excel). Since the calculated value of F is less than this, we conclude that the variance is consistent between the two reactors.
The pooled variance is then calculated.
sp2 = [(9-1)0.994 + (8-1) 0.480]/(9 + 8 – 2) = 0.754
The next step is to calculate the sdiff =.
sdiff =SQRT[0.754((1/9)+(1/8))] = 0.422
The t value for α = 0.05 and 15 degrees of freedom is (using the TINV function in Excel):
t = 2.13
The 100 (1 – α)% confidence interval for μ1– μ2is given by
X1 – X2 ± tsdiff
92.68 – 92.18 ± 2.13(0.422)
0.5 ± 0.9
The 95% confidence interval for μ1– μ2is given by:
0.5 – 0.9 < μ1– μ2 < 0.5 + 0.9
-0.4 < μ1– μ2 < 1.4
Since the interval contains zero, we conclude that there is no evidence that the two reactors are operating at different yields.
Remember that this technique represents a snapshot in time of the processes. If the processes are not stable, you cannot be sure of getting a similar result in the future.
Summary
This newsletter demonstrated how to compare two processes. The first step is to check if the variances of the two processes are the same by comparing the variances and using an F test to determine if they are the same. If they are, an estimate of the standard deviation is found from the combined data. The t distribution is used to put a confidence interval around the difference in means. If the confidence interval contains 0, we conclude that there is no difference in the means. If the confidence interval does not contain zero, we conclude that there is a difference in means.