November 2021
(Note: all the previous SPC Knowledge Base in the comparing processes category are listed on the right-hand side. Select this link for information on the SPC for Excel software.)
 Sometimes there is a need to compare processes to see if they are the same or they are different. The question you should ask is the same or different with respect to what? Two basic ways processes can differ are in terms of the average and the amount of variation. The Levene’s test is used to evaluate if multiple processes have the same (equal) variances. It is answering the question:
Sometimes there is a need to compare processes to see if they are the same or they are different. The question you should ask is the same or different with respect to what? Two basic ways processes can differ are in terms of the average and the amount of variation. The Levene’s test is used to evaluate if multiple processes have the same (equal) variances. It is answering the question:
Do one or more of the processes have a significantly different variance than the other processes?
In this issue:
- Introduction
- The Hypotheses
- Levene’s Statistic
- The Data
- The Calculations
- Deciding if the Variances are the Same
- Will Control Charts Help in this Analysis?
- Summary
- Quick Links
Please feel free to leave a comment at the end of this newsletter. You may also download a pdf copy of this newsletter at this link.
Introduction
The modified Levene’s test for equality of variances determines if processes are operating at the “same” variance. Of course, things vary as we know, so the variances calculated from different processes will not be identical. But this does not mean that they are statistically different. The modified Levene’s test is used to determine if the differences in variances are statistically significant.
There is another test that also checks for equality of variances. It is called Bartlett’s test. The modified Levene’s test is less sensitive than Bartlett’s test when the data are not normally distributed. In this case, use the modified Levene’s test. However, if the data are normally distributed or symmetrical, you should use Bartlett’s test. Please see our SPC Knowledge Base article, Bartlett’s Test for Equality of Variances, for more information on Bartlett’s test.
There is also a more visual method of checking for equality of variances. It is the analysis of ranges method. For more information on this technique, see our SPC Knowledge Base article, The Analysis of Means and Ranges.
Our SPC for Excel software performs the calculations for the modified Levene’s test automatically as well as for Bartlett’s test and the Analysis of Means and Ranges. Let’s dig deeper into the calculations behind the Levene’s test.
The Hypotheses
Suppose we have k processes that are used to make the same material. These processes are often referred to as treatments. Levene’s test is just that – a test. So, with a test, there must be something we are trying to prove or disprove. These are given by the null and alternate hypotheses. The null hypothesis for k treatments is given by:
H0: σ12= σ22= …. = σk2
whereσi2is the variance of the ith treatment. The null hypothesis is that all treatments have the same variance.
The alternate hypothesis is given by:
H1: σi2≠ σj2for at least one i and j
The alternate hypothesis is that at least two of the treatment variances are statistically different – they are not all equal.
Levene’s Statistic
The calculations primarily involve computing Levene’s statistic and then comparing this statistic to a critical value or a p value. This statistic is denoted by FLevene and is given by:
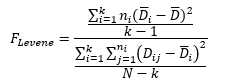
where k = number of treatments, ni = number of results for the ith treatment, and N is the total number of results across the k treatments.
Dij is the absolute deviation of observation j (Yij) from the ith treatment median (Ãi):
Dij = |Yij-Ãi|
Di is the average of the ni absolute deviations for treatment i.
D is the average of all N absolute deviations.
It is the use of the median in Dij that makes this the “modified” Levene’s Test. You could use the treatment average in place of the median.
The Data
Consider a situation where you are examining four different treatments that are used to produce the same material. Note that a “treatment” can be as simple as changing operating conditions, raw materials, etc. Fifteen samples are taken from each treatment. The results are shown in Table 1. The four treatments are A, B, C and D
Table 1: Treatment Data
| Sample | A | B | C | D |
|---|---|---|---|---|
| 1 | 95.5 | 95.6 | 95.8 | 65.7 |
| 2 | 93.0 | 119.5 | 101.6 | 95.5 |
| 3 | 79.9 | 95.0 | 103.1 | 71.2 |
| 4 | 97.9 | 82.3 | 113.3 | 87.8 |
| 5 | 92.7 | 88.1 | 95.3 | 96.4 |
| 6 | 84.0 | 102.9 | 96.1 | 132.4 |
| 7 | 95.4 | 97.1 | 100.7 | 129.4 |
| 8 | 100.5 | 95.8 | 105.8 | 91.7 |
| 9 | 91.2 | 92.3 | 103.0 | 104.1 |
| 10 | 90.9 | 101.8 | 91.0 | 85.4 |
| 11 | 115.3 | 100.4 | 99.7 | 100.1 |
| 12 | 104.5 | 116.7 | 110.3 | 69.2 |
| 13 | 91.5 | 96.8 | 92.8 | 85.6 |
| 14 | 103.2 | 110.2 | 102.6 | 94.6 |
| 15 | 111.2 | 117.5 | 99.9 | 112.5 |
There are total of sixty results (N) over the 4 treatments (k).
The Calculations
The calculated average, standard deviation, and variance for the four treatments are shown in Table 2.
Table 2: Treatment Summary Statistics
| Statistic | A | B | C | D |
|---|---|---|---|---|
| Average | 96.45 | 100.80 | 100.73 | 94.77 |
| Std. Dev. | 9.42 | 10.91 | 6.12 | 19.52 |
| Variance | 88.68 | 119.03 | 37.49 | 380.90 |
You can see that the variance in treatment D appears to be much larger than the others. But is this sufficient “proof” that the variance for treatment D is significantly different from the other three? Treatment C has the smallest variance. Is that “proof” that the variance for treatment C is significantly different from the other three?
No, this is not sufficient proof that the variances are different. We will use the modified Levene’s test to determine if the variances are the same using the data in Table 1.
The test involves calculating Levene’s statistic as shown in the equation above. The first step is to find the median for each treatment. You can use Excel’s MEDIAN function to do this. The medians are given below:
- Treatment A: 95.4
- Treatment B: 97.1
- Treatment C: 100.7
- Treatment D: 94.6
The next step is to calculate the absolute difference between each individual result in the treatment and the treatment median. For example, the first sample result for Treatment A is 95.5. The median for Treatment A is 95.4. The equations below use 1 for Treatment A, 2 for Treatment B, etc. The absolute deviation of this sample result from the treatment median is:
D11 = |Y11-Ã1 | = |95.5 – 95.4| = 0.1
The first sample result for Treatment B is 95.6. The median for Treatment B is 97.1. The absolute deviation of this sample result from the treatment median is:
D12 = |Y12– Ã2| = |95.6 – 97.1| = 1.5
Table 3 contains the absolute deviations from the medians for all the results.
Table 3: Absolute Deviations from Treatment Medians
| Sample | A | B | C | D |
|---|---|---|---|---|
| 1 | 0.1 | 1.5 | 4.9 | 28.9 |
| 2 | 2.4 | 22.4 | 0.9 | 0.9 |
| 3 | 15.5 | 2.1 | 2.4 | 23.4 |
| 4 | 2.5 | 14.8 | 12.6 | 6.8 |
| 5 | 2.7 | 9.0 | 5.4 | 1.8 |
| 6 | 11.4 | 5.8 | 4.6 | 37.8 |
| 7 | 0.0 | 0.0 | 0.0 | 34.8 |
| 8 | 5.1 | 1.3 | 5.1 | 2.9 |
| 9 | 4.2 | 4.8 | 2.3 | 9.5 |
| 10 | 4.5 | 4.7 | 9.7 | 9.2 |
| 11 | 19.9 | 3.3 | 1.0 | 5.5 |
| 12 | 9.1 | 19.6 | 9.6 | 25.4 |
| 13 | 3.9 | 0.3 | 7.9 | 9.0 |
| 14 | 7.8 | 13.1 | 1.9 | 0.0 |
| 15 | 15.8 | 20.4 | 0.8 | 17.9 |
The next step is to calculate the average of the absolute deviations for each treatment. This is denoted by Di . The average for each treatment is given below:
- Treatment A: 6.99
- Treatment B: 8.21
- Treatment C: 4.61
- Treatment D: 14.25
Another value needed to complete the calculation is D, which is the average of all the absolute deviations. This value is 8.52.
Look at the last two sets of averages: the four individual treatments and the overall. Can you begin to draw some conclusions? It is clear that Treatment D has the largest deviation. This means there is more variation in Treatment D than the other three.
Treatment C has the smallest deviation. This means there is less variation in Treatment C than the other three. Do we conclude that these are “real” differences?
Everything varies. We aren’t going to get the same result each time. The question is:
Are any of these differences statistically significant?
The modified Levene’s test is going to answer that for us.
The numerator in Levene’s statistic is:
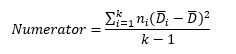
For each treatment, you need the average absolute deviation for that treatment minus the overall average absolute deviation. The numerator is given by:
Numerator= 15[(6.99-8.52)2+(8.21-8.52)2+(4.61-8.52)2+(14.25-8.52)2]/(4-1) = 252.79
The denominator in Levene’s statistic is:
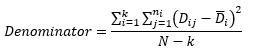
Once again, consider the first sample for Treatment A. The value of D11 was found above in Table 3. It is 0.1. The value of the average absolute deviation for this treatment (6.99) is then subtracted from D11. Then:
(Dij–Di )2=(0.1-6.99)2=47.47
Table 4 shows these calculations for each result.
Table 4: Square of Deviation of Each Result from the Treatment Median
| Sample | A | B | C | D |
|---|---|---|---|---|
| 1 | 47.47 | 45.02 | 0.08 | 214.62 |
| 2 | 21.07 | 201.36 | 13.76 | 178.22 |
| 3 | 72.42 | 37.33 | 4.88 | 83.72 |
| 4 | 20.16 | 43.43 | 63.84 | 55.50 |
| 5 | 18.40 | 0.62 | 0.62 | 155.00 |
| 6 | 19.45 | 5.81 | 0.00 | 554.60 |
| 7 | 48.86 | 67.40 | 21.25 | 422.30 |
| 8 | 3.57 | 47.75 | 0.24 | 128.82 |
| 9 | 7.78 | 11.63 | 5.34 | 22.56 |
| 10 | 6.20 | 12.32 | 25.91 | 25.50 |
| 11 | 166.67 | 24.11 | 13.03 | 76.56 |
| 12 | 4.45 | 129.73 | 24.90 | 124.32 |
| 13 | 9.55 | 62.57 | 10.82 | 27.56 |
| 14 | 0.66 | 23.91 | 7.34 | 203.06 |
| 15 | 77.62 | 148.60 | 14.52 | 13.32 |
The sum of the values in Table 4 is 3878.11. The denominator then becomes:
Denominator=3878.11/(60-4)=69.25
Levene’s statistic is then given by:
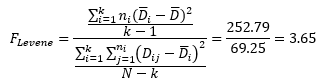
Finally, we have the value of Levene’s statistic. Now what does it mean? Is it significant? Are the variances the same?
Deciding if the Variances are the Same
There are two ways to determine if the variances are the same based on Levene’s statistic. One is to compare it to a critical value of F (from the F distribution) based on the degrees of freedom in the numerator and in the denominator as well as the value of a, which you choose. The most common significance level is usually a = .05 (corresponds to a 95% confidence level). The critical value of F is then given as Fa, k-1, N-k and k–1 is the degrees of freedom in the numerator and N–k is the degrees of freedom in the denominator. You can use FINV in Excel to determine this value:
Fcritical =Fa, k-1, N-k = FINV(0.05, 3, 56) = 2.77
If FLevene is greater than or equal to Fcritical, then there is evidence that the variances are not the same. The null hypothesis would be rejected. In this example, FLevene is 3.65 which is greater than 2.77, so you conclude the variances are not the same.
You can also use the p value approach to determine if the variances are the same. If the p value is less than or equal to the value of a you selected, then the variances are not the same. You can use the FDIST function in Excel to calculate the p value as follows:
p value = FDIST(Levene’s statistic, k-1, N-k) = FDIST(3.65, 3, 56) = 0.018
Since 0.018 is less than 0.05, our value of a, we conclude that the variances are not equal.
So, based on our analysis, we conclude that the four processes are not operating at the same variance.
Will Control Charts Help in this Analysis?
Levene’s test does not provide a visual picture of what is going on. Will control charts help in this analysis? Most likely. An individuals chart (X-mR) is used next to see what control charts tell us about the four treatments. Figure 1 shows the X chart for the four treatments combined. The chart is divided into four zones for treatment A, B, C and D.
Figure 1: X Chart for the Four Treatments
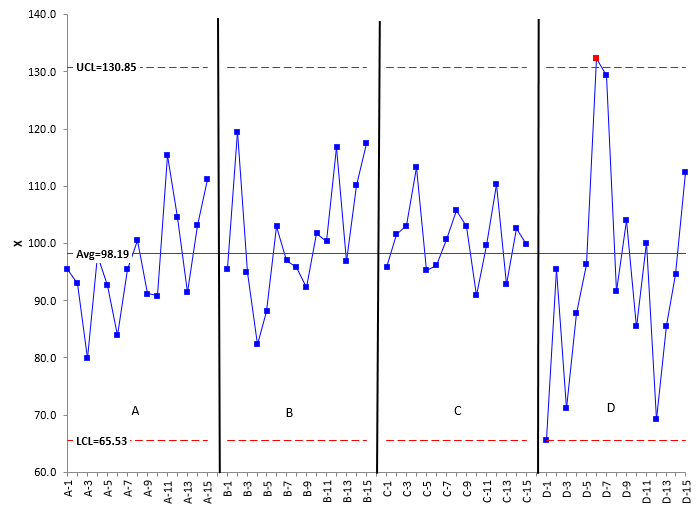
What does Figure 1 tell you about the four treatments? They appear to be operating around the same average, no significant difference. But there seems to be more spread in the data for treatment D. In fact, there is an out of control point for Treatment D when you consider all treatments in calculating the average and control limits. The moving range chart should confirm the more variation in Treatment D. The moving range chart is shown in Figure 2.
Figure 2: Moving Range Chart for the Four Treatments
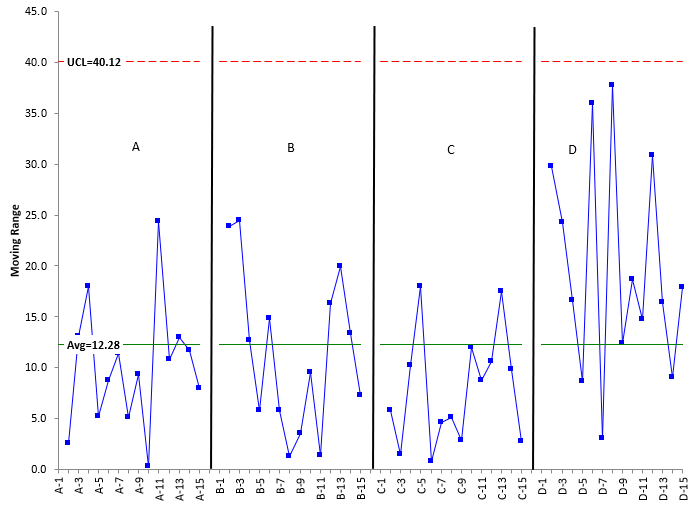
It is clear from Figure 2 that treatment D has more variation than the other three. You could do a X-mR chart for each treatment. If you did, you would find that each treatment is in statistical control (consistent and predictable) and the average moving ranges (mR)for the four treatments are:
- Treatment A: 10.11
- Treatment B: 11.44
- Treatment C: 7.86
- Treatment D: 19.71
Treatment D definitely has a larger average moving range. To estimate sigma, you divide the average moving range by 1.128. Then you square sigma to estimate the variance. The results are shown in Table 5. The first two entries are the calculated standard deviation and variance from Table 2. The average moving range is listed, then the estimated value of sigma from the average moving range, and the estimated variance as the square of sigma.
Table 5: Comparison of Calculated Statistics and Estimated from Moving Range Chart
| Statistic | A | B | C | D |
|---|---|---|---|---|
| Std. Dev. | 9.42 | 10.91 | 6.12 | 19.52 |
| Variance | 88.68 | 119.03 | 37.49 | 380.90 |
| mR | 10.11 | 11.44 | 7.86 | 19.71 |
| Sigma | 8.96 | 10.14 | 6.97 | 17.47 |
| Est. Variance | 80.28 | 102.82 | 48.58 | 305.2 |
The calculated and estimated statistics are fairly close and show the same pattern. Treatment D appears to have more variation than the other three treatments. Control charts, as usual, do provide insights into the process.
Summary
This publication examined how the modified Levene’s test for equality of variances is performed. It is useful when there are departers from normality.
Levene’s statistic is calculated and compared to either a critical value of F or to a p value to see if there is reason to reject the null hypothesis that all the variances are equal. There are alternatives to this test, in particular the Analysis of Means and Ranges and Bartlett’s test.