October 2018
(Note: all the previous SPC Knowledge Base in the experimental design category are listed on the right-hand side. Select this link for information on the SPC for Excel software.)

Experimental design techniques help you do this – and if there are lots of potential factors, then fractional factorial designs are a great help in reducing the number of runs required. Of course, there are some things you “lose” with fewer runs. The effects of factors and interactions are “confounded” with other factors or interactions.
This month’s publication continues our look at two-level fractional factorial experimental designs. We will look at a five-factor example and show how to analyze and interpret the results. In this example, the results allow us to re-analyze the results as a full factorial design. In this publication:
- Review of Part 1
- Example Experimental Design
- Analysis and Interpretation of Results
- Re-analysis of Results as a Full Factorial Design
- Summary
- Quick Links
Review of Part 1
Full factorial designs allow you to estimate the effect that all factors and their interactions have on a response, such as product purity above. This sounds like a great approach – and it is – when you can use it. The problem is that as the number of factors increase, the number of runs required increases very rapidly. For a full factorial, the number of runs required, with no replication, is given by 2k where k is the number of factors.
So, for 3 factors, eight runs are required; for 4 factors, sixteen runs are required, and for 5 factors, 32 runs are required for a full factorial design. And, since you usually want to replicate runs to estimate the experimental error, the number of runs quickly becomes prohibitive in most cases.
This is where fractional factorials enter the picture. Quite often, the information you need can be obtained by running only a fraction of the full factorial. You don’t have to estimate the effects of all factors and interactions all the time. And there tends to be a hierarchy of effects. In general, main effects are more significant than two-factor interactions which are more significant than three-factor interactions, etc.
The higher order interactions often tend to become insignificant and can be ignored. In addition, not all factors in a design with many factors will be significant. If the number of factors is large, there are often factors and interactions that are not significant. We don’t need to do all those runs in the full factorial. Anytime there are four or more factors, a fractional factorial design should be considered.
Part 1 of this publication described how a fractional factorial is set up. It is often a ½ or ¼ of a full factorial design. Part 1 also described how to determine which factor and interactions are confounded. If two interactions/factors are confounded, you can’t tell how much of the effect is due to each one. Part 1 also defined the resolution of a design – which gives us more insight to the confounding pattern.
Example Experimental Design
Suppose you want to maximize the yield of a given reaction. There are five factors which you feel are important. These are given below.
- Feed rate (10-15 liters/min)
- Catalyst (1-2 wt.%)
- Agitation rate (100-120 rpm)
- Temperature (140-180 deg C)
- Concentration (3-6 wt.%)
A full factorial design would require 25 = 32 runs (with no replications). This is too many runs for operations to be willing to handle. You decide to go with 16 runs and use a 25-1 fractional factorial. This is a resolution V design and does not confound main effects and two order interactions but does confound two order interactions with third order interactions. Part 1 of this publication describes how to determine what factors and interactions are confounded. For this design, the following factors and interactions are confounded:
A = BCDE
B = ACDE
C = ABDE
D = ABCE
E = ABCD
AB = CDE
AC = BDE
AD = BCE
AE = BCD
BC = ADE
BD = ACE
BE = ACD
CD = ABE
CE = ABD
DE = ABC
The experimental runs were randomized and analyzed for reaction yield. The results are shown in Table 1 in standard run order.
Table 1: Reaction Yield Fractional Factorial Results
| Run | A | B | C | D | E | Yield |
|---|---|---|---|---|---|---|
| 1 | 10 | 1 | 100 | 140 | 6 | 56 |
| 2 | 15 | 1 | 100 | 140 | 3 | 53 |
| 3 | 10 | 2 | 100 | 140 | 3 | 63 |
| 4 | 15 | 2 | 100 | 140 | 6 | 65 |
| 5 | 10 | 1 | 120 | 140 | 3 | 53 |
| 6 | 15 | 1 | 120 | 140 | 6 | 55 |
| 7 | 10 | 2 | 120 | 140 | 6 | 67 |
| 8 | 15 | 2 | 120 | 140 | 3 | 61 |
| 9 | 10 | 1 | 100 | 180 | 3 | 69 |
| 10 | 15 | 1 | 100 | 180 | 6 | 45 |
| 11 | 10 | 2 | 100 | 180 | 6 | 78 |
| 12 | 15 | 2 | 100 | 180 | 3 | 93 |
| 13 | 10 | 1 | 120 | 180 | 6 | 49 |
| 14 | 15 | 1 | 120 | 180 | 3 | 60 |
| 15 | 10 | 2 | 120 | 180 | 3 | 95 |
| 16 | 15 | 2 | 120 | 180 | 6 | 82 |
The results in Table 1 were analyzed using the SPC for Excel software. The analysis and interpretation are given below.
Analysis and Interpretation of Results
The first step in analysis of the results is to calculate the effects of the factors and interactions. The effect is a measure of how much that factor or interaction impacts the response variable, reaction yield.
An effect can be viewed as the average response when a factor is at its high level minus the average response when a factor is at its low level with all other factors held constant. Please see an earlier publication for more information on effects and how to calculate them.
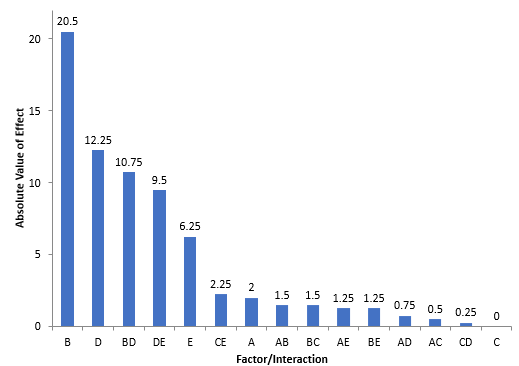
The effects for this example are shown in Figure 1. The absolute value of the effects is plotted. Factor B has the biggest effect followed by Factor D. Factor C has no effect on the results. So, the larger the effect, the more likely it is to be statistically significant. Analysis of Variance (ANOVA) is used to help determine which are statistically significant mathematically.
Figure 1: Pareto Diagram of Absolute Value of Effects
Usually, an effect is not zero even if it does not impact the result. This is because our processes have variation. You often replicate the experimental runs, so you can estimate the process variation – the experimental error. This is usually done using ANOVA. The ANVOA table for this design is shown in Table 2.
Table 2: ANOVA Table for Reaction Yield DOE
| Source | SS | df | MS | F | p value | % Contribution |
|---|---|---|---|---|---|---|
| A | 16.00 | 1 | 16.00 | N/A | N/A | 0.48% |
| B | 1681.0 | 1 | 1681.0 | N/A | N/A | 50.47% |
| C | 0.000 | 1 | 0.000 | N/A | N/A | 0.00% |
| D | 600.3 | 1 | 600.3 | N/A | N/A | 18.02% |
| E | 156.3 | 1 | 156.3 | N/A | N/A | 4.69% |
| AB | 9.000 | 1 | 9.000 | N/A | N/A | 0.27% |
| AC | 1.000 | 1 | 1.000 | N/A | N/A | 0.03% |
| AD | 2.250 | 1 | 2.250 | N/A | N/A | 0.07% |
| AE | 6.250 | 1 | 6.250 | N/A | N/A | 0.19% |
| BC | 9.000 | 1 | 9.000 | N/A | N/A | 0.27% |
| BD | 462.3 | 1 | 462.3 | N/A | N/A | 13.88% |
| BE | 6.250 | 1 | 6.250 | N/A | N/A | 0.19% |
| CD | 0.250 | 1 | 0.250 | N/A | N/A | 0.01% |
| CE | 20.25 | 1 | 20.25 | N/A | N/A | 0.61% |
| DE | 361.0 | 1 | 361.0 | N/A | N/A | 10.84% |
| Error | 0.000 | 0 | ||||
| Total | 3331.0 | 15 |
Since the runs in this experimental design were not replicated, there is no way to estimate the experimental error and thus no way to calculate the F values and p values that are normally used to determine if a factor or interaction is statistically significant. For more information on using ANOVA to interpret experimental design results, please see our publication at this link.
There are two other ways to judge which factors and interactions might be significant when the experimental runs were not replicated. One is to examine the % Contribution column in Table 2. This column gives the percent of the total sum of squares due to the factor or interaction. Sum of squares are a measure of variation. Those that are greater than 5% might be significant. The following interactions might be significant: B, D, BD and DE. Factor E is very close to the 5% and may be significant, particularly with the fact that the DE interaction term appears to be significant.
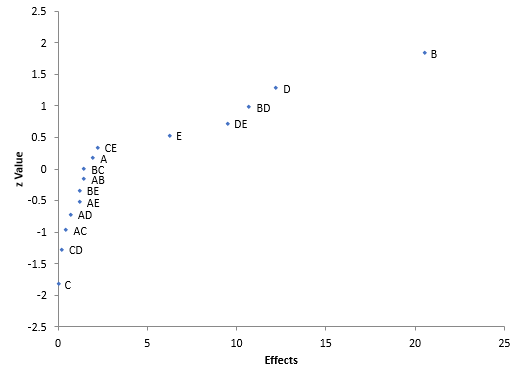
You can also examine the half-normal plot of effects. This plot is shown in Figure 2. This type of chart plots the absolute value of the effect versus its z-value. The effects that are further from 0 could be statistically significant. From this plot, it looks like B, D, E, BD and DE are significant – confirmation of what was seen above.
Figure 2: Half-Normal Plot of Effects
Based on these results, you can build a model that predicts the results for reaction yield. The model below is based on the coded levels of the factors. This simply puts all the factors on a level from -1 (low level) to +1 (high level). The coefficient of each term is ½ the effect for that term. The larger the coefficient, the larger the impact of that term on the response variable. For more information on building the model and the coding of factors, please see this link. The model for these results is:
Reaction Yield = 65.250 + 10.250(B) + 6.125(D) – 3.125(E) + 5.375(BD) – 4.750(DE)
The goal is to maximize the yield. You select the levels of the factors so that the above model is maximized. The maximum yield occurs when B = 1, D = 1, and E = -1. You can estimate that maximum yield as:
Reaction Yield = 65.250 + 10.250(1) + 6.125(1)- 3.125(-1) + 5.375(1)(1) – 4.750(1)(-1) = 91.125
We have determined which factors and interactions are significant by using a fractional factorial design and running half the runs we would have needed for a full factorial design. You always need to make confirmation runs to ensure that the experimental design analysis was correct. In this case, simply put the factors at the levels indicated above and do several runs to confirm the reaction yield is around 91%.
Re-analysis of Results as a Full Factorial Design
In the example above, there were initially five factors that were thought to impact the reaction yield. A fractional factorial design was run, and it was discovered that only three of the five factors had a significant impact. In the design above, the experimental runs were not replicated.
Sometimes when there are factors that are not significant, it might be possible to re-analyze the results as a full factorial design. This happens to be true in this case. Table 3 shows the runs re-arranged into a three-factor full factorial design, now with one replication.
Table 3: Three Factor Full Factorial Design
| B | D | E | Result 1 | Result 2 |
|---|---|---|---|---|
| 1 | 140 | 3 | 53 | 53 |
| 2 | 140 | 3 | 63 | 61 |
| 1 | 180 | 3 | 69 | 60 |
| 2 | 180 | 3 | 93 | 95 |
| 1 | 140 | 6 | 56 | 55 |
| 2 | 140 | 6 | 65 | 67 |
| 1 | 180 | 6 | 45 | 49 |
| 2 | 180 | 6 | 78 | 82 |
Since the runs are replicated, the analysis of variance analysis will include the experimental error term. The ANOVA table for this design is shown in Table 4.
Table 4: ANOVA Table for Three Factor Full Factorial Analysis
| Source | SS | df | MS | F | p value | % Contribution |
|---|---|---|---|---|---|---|
| A | 1681.0 | 1 | 1681.0 | 213.460 | 0.0000 | 50.47% |
| B | 600.3 | 1 | 600.3 | 76.222 | 0.0000 | 18.02% |
| C | 156.3 | 1 | 156.3 | 19.841 | 0.0021 | 4.69% |
| AB | 462.3 | 1 | 462.3 | 58.698 | 0.0001 | 13.88% |
| AC | 6.250 | 1 | 6.250 | 0.794 | 0.3990 | 0.19% |
| BC | 361.0 | 1 | 361.0 | 45.841 | 0.0001 | 10.84% |
| ABC | 1.000 | 1 | 1.000 | 0.127 | 0.7308 | 0.03% |
| Error | 63.00 | 8 | 7.875 | 1.89% | ||
| Total | 3331.0 | 15 | 100.00% |
When replicates are run, the key column to examine is the p-value column. Those sources with p-values less than 0.05 are statistically significant. In this table, that is true for B,D, E, BD and DE. So, these are statistically significant. This matches what we found before with the fractional factorial design.
Summary
This publication has provided an example of a fractional factorial design as well as a review of how to analyze and interpret the results. Since not all factors were significant, it was possible to re-analyze the results as a full factorial design.