February 2019
(Note: all the previous SPC Knowledge Base in the basic statistics category are listed on the right-hand side. Select this link for information on the SPC for Excel software.)
 This month’s publication introduces nonparametric techniques for a single sample. Over the years, we have produced several publications involving analyzing sample results. For example, you might want to determine if the mean of a process is a certain value. To do that, you take samples from the process and then compare the results using either a t-test or a z-test. Many statistical techniques, like the t-test and z-test for a mean, are based on the assumption that your data are normally distributed.
This month’s publication introduces nonparametric techniques for a single sample. Over the years, we have produced several publications involving analyzing sample results. For example, you might want to determine if the mean of a process is a certain value. To do that, you take samples from the process and then compare the results using either a t-test or a z-test. Many statistical techniques, like the t-test and z-test for a mean, are based on the assumption that your data are normally distributed.
The assumption of normality is often simply ignored. But there are times when this assumption is not valid. For example, lifetime data (such as product survival times) are not normally distributed. Neither are data involving call center waiting times, bacterial growth, or the number of injuries in a plant. What do you do when the assumption of normality is not valid?
There are techniques called nonparametric statistical methods that can be used when the data are not normal. These techniques are distribution-free; they make no assumptions about the distribution from which you take the sample.
In this issue:
- Introduction to Nonparametric Techniques
- Sign Test and Confidence Interval
- Wilcoxon Signed Rank Test
- Summary
- Quick Links
Please feel free to leave a comment below. You can download a pdf copy of this publication at this link.
Introduction to Nonparametric Techniques
Nonparametric techniques are statistical methods that are distribution-free. You don’t have the assumption that the data are normally distributed. One major difference between nonparametric techniques and those requiring normally distributed data is the use of the median instead of the average. The nonparametric techniques will make use of the median, which will be denoted by ũ. The median gives a better estimate of the center than the average for non-normal distributions.
We will cover two nonparametric techniques below. These deal with a single sample and discovering something about the population median being sampled. The example data and the mathematical equations to do the analysis come from the book “Statistics and Data Analysis: From Elementary to Intermediate” by Ajit Tamhane and Dorothy Dunlop.
Sign Test for a Single Sample
In this test, a random sample is taken from a population. The results are then used to determine if the population median is equal to some value or different from some value. For example, a sample of ten thermostats are taken at random from a production lot. The design setting for these thermostats is 200. We want to know if this is true for the production lot. So, each thermostat is tested. The results are given below.
Table 1: Thermostat Setting Data
| Setting |
|---|
| 202.2 |
| 203.4 |
| 200.5 |
| 202.5 |
| 206.3 |
| 198.0 |
| 203.7 |
| 200.8 |
| 201.3 |
| 199.0 |
The sign test for a single sample is used below to see if the population median, based on this sample, is 200. Using the statistics hypothesis route, we are testing the following hypotheses:
H0:ũ=ũ0= 200
H1:ũ<>ũ0= 200
where H0 is the null hypothesis and H1 is the alternate hypothesis. Note that if the null hypothesis is true, then the probability of a sample being larger or smaller that ũ0is ½ or 0.5. The sign test methodology is straightforward. There are essentially three steps:
- Count the number of individual results (xi) that are larger than ũ0. This is the number of plus signs and is denoted by s+.
- Count the number of individual results (xi) that are smaller than ũ0. This is the number of minus signs and is denoted by s-.
- Reject HO if s+ is large or if s- is small
The first steps are easy to do. In this example, s+ is 8, while s- is 2. There are 8 values greater than 200 and 2 values less than 200. Step 3 is the one where you make your decision though. Like many statistical tests, you must select the probability of making a mistake. This usually focuses on the alpha value (α). It is the probability of rejecting the null hypothesis when it is actually true. Typical values of α include 0.05 and 0.01. You decide that you want α to be 0.05. This means that there is only a 5% chance of rejecting the null hypothesis when it is true.
How do you decide to accept or reject the null hypothesis? One way to do this is to assume that the null hypothesis is true and then determine the probability (p value) of getting the sample result. If the p value is large, it means that there is a large probability of getting the sample result when the null hypothesis is true, and you will accept that the null hypothesis is probably true. But if the probability of getting the sample result is small, you will assume that the null hypothesis is probably not true and reject it in favor of the alternative hypothesis. The small is what α controls.
You can calculate the p value for the sign test by using the binomial distribution. With this distribution, there are only two possible outcomes. In our example, it is either larger than or less than 200.
The p-value is given by the following equation:
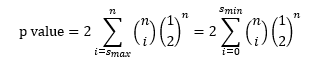
where n = sample size, smax= max(s+, s-) and smin= min(s+,s-). In Excel, you don’t have to perform the calculation shown in the equation above. You can use the BINOMDIST or BINOM.DIST functions with the equation above with the smin.
p value = 2* BINOMDIST(smin, n, p, TRUE) = 2*BINOMDIST(2,10, 0.5, TRUE) = 0.110.
The p value for the data is 0.110. This is larger than 0.05, the value of α we selected. The conclusion is that the thermostat design setting is not different from 200. We accept the null hypothesis.
You can also construct a confidence interval to see if the design setting of 200 lies in the confidence interval. The confidence intervals are a little different with this type of test than with, for example, the t-test. Since this is binomial data, you can’t have an exactly 95% confidence interval (based on 1 – α). However, you can use the cumulative binomial probabilities to determine the confidence interval. It has the following form:
X(b+1)≤ũ≤ X(n-b)
where b is the lower α /2 critical point of the binomial distribution.
The first step in finding the confidence interval is to sort the data in ascending order. This is shown in Table 2.
Table 2: Sorted Thermostat Setting Data
| Number | Setting |
|---|---|
| 1 | 198.0 |
| 2 | 199.0 |
| 3 | 200.5 |
| 4 | 200.8 |
| 5 | 201.3 |
| 6 | 202.2 |
| 7 | 202.5 |
| 8 | 203.4 |
| 9 | 203.7 |
| 10 | 206.3 |
To find the confidence interval, start with the first thermostat setting and calculate the following:
1 – α = 1 – 2 * BINOMDIST(b, 10, 0.5, True) = 0.9785 or 97.85%
where b= 1. The 97.85% confidence interval is then given by:
X(b+1)≤ũ≤ X(n-b)
X2≤ũ≤ X9
199 ≤ũ≤ 203.7
Now go to the second point and do the following calculation:
1 –α= 1 – 2 * BINOMDIST(2, 10, 0.5, True) = 0.8906 or 89.06%
So, 89.06% confidence interval is given by the third and eight results in the table: 200.5 to 203.4.
The output from the SPC for Excel program for this data is shown below.
Figure 1: Sign Test Output

What happens if the sample result is equal to the design setting (ũ0)? The process above assumes that this does not happen. But, of course, it can happen. The easiest thing to do is to ignore ties and just use the rest of the data. This does impact the sample size of course, but it is rare that there will be many samples that equalũ0. If there are, then the null hypothesis is probably true – or your measurement system needs some work because it can’t tell the difference between samples.
.
Wilcoxon Signed Rank Test
The Wilcoxon Signed Rank Test is another parametric method to analyze sample results taken from a non-normal distribution. In general, the steps are:
- Calculate the absolute value of each sample result fromũ0: di= |xi-ũ0|
- Rank order the differences with ri = the rank of di
- Calculate w+ which is the sum of the ranks of the positive differences
- Calculate w- which is the sum of the ranks of the negative differences
- Reject HO if w+ is large or if w- is small
Once again, you have to calculate the p value to determine if w+ is considered large or if w- is considered small. This involves the use of the null distribution. We will continue to use the thermostat data from Table 1.
Table 3 shows the thermostat data with the differences and the ranks.
Table 3: Wilcoxon Signed Rank Test Rankings
| Setting | Difference from 200 | |Difference| | Rank |
|---|---|---|---|
| 200.5 | 0.5 | 0.5 | 1 |
| 200.8 | 0.8 | 0.8 | 2 |
| 199.0 | -1.0 | 1.0 | 3 |
| 201.3 | 1.3 | 1.3 | 4 |
| 198.0 | -2.0 | 2.0 | 5 |
| 202.2 | 2.2 | 2.2 | 6 |
| 202.5 | 2.5 | 2.5 | 7 |
| 203.4 | 3.4 | 3.4 | 8 |
| 203.7 | 3.7 | 3.7 | 9 |
| 206.3 | 6.3 | 6.3 | 10 |
You can now calculate w+ and w-. w- is the sum of the ranks for those differences that are negative. There are only two differences that are negative. The sum of the ranks is 3 + 5 = 8. So, w- is 8. To find w+, you sum the ranks of the positive differences. The result is w+ = 47
To calculate the p value, you use the null distribution to determine the p value:
p value = 2* P{W ≥ w+)
You have to look up this probability from a table of the upper probabilities of the null distribution of the Wilcoxon Signed Range statistic. You can download this table at this link. This table handles samples up to 20. The probability from the table is 0.024. Thus,
p value = 2(0.024) = 0.048.
Note that p value calculated for the Wilcoxon Ranked Sign test is less than α= 0.05 – so we conclude that the population median is different than 200. The Sign Test did not find a difference.
The Wilcoxon Signed Rank Test has two types of ties. One is when the sample result equals ũ0. Like the sign test, these are ignored. The other tie is when several |di| values have the same rank. In this case, you assign an average rank to them. For example, suppose the first two |di| values are the same and ranked 1 and 2. Then the average range for both is 1.5.
You can calculate a confidence interval as well, but it involves looking at all pairwise averages. We will not do that here.
Figure 2 shows the output for this test using the SPC for Excel software.
Figure 2: Wilcoxon Signed Rank Test Output

Summary
This publication examined two methods for analyzing single samples taken from non-normal distributions. One method is the Sign Test. This method involves looking at the number of sample results above ũ0and the number of sample results below ũ0. The other method is the Wilcoxon Signed Rank Test. This method involves examining the distances the sample results are from ũ0. Both tests focus on the median, not the average.
Your two tests give different results. What do hou make of this?
Two different statistical techniques based on different things – one the number above or below the median, the other on the distance from the median. For me, if the p-value is between 0.05 and .2, i think you need more data to make a decision. Bu two different statistical tests will give different answers.
This is exactly the information I was looking for! At least, the answer really came from your comment. I had two different results from the two tests, and didn't know if that was normal or not.