Acceptance Criteria for Measurement Systems Analysis (MSA)

April 2018

(Note: all the previous publications in the measurement systems analysis category are listed on the right-hand side. Select “Publications” to go to the SPC Knowledge Base homepage. Select this link for information on the SPC for Excel software.)

You have run your Gage R&R study. You enter the results into your software program. You run the analysis. The results come back that the % Gage R&R is 32%. You look at the acceptance criteria from AIAG:

• If the % Gage R&R is under 10%, the measurement system is generally considered to be an adequate measurement system.
• If the % Gage R&R is between 10 % to 30%, the measurement system may be acceptable for some applications.
• If the % Gage R&R is over 30%, the measurement system is considered to be unacceptable.

So, since your % Gage R&R is 32%, your measurement system is unacceptable, correct? No, that is not the case at all. In fact, you should NEVER use the acceptance criteria listed above. It is misleading and not based on the realities of how the measurement system impacts your process.

This month’s publication looks at the criteria for rating the usefulness of a measurement system. Of course, in the end, that is between you and your customer. But there are much better guidelines available than those used by AIAG. These better guidelines have been developed by Dr. Donald Wheeler. Dr. Wheeler divides a measurement system into four categories – First Class monitors, Second Class monitors, Third Class monitors and Fourth Class monitors. These categories give insight into these three characteristics of the measurement system:

1. How much the measurement system reduces the strength of a signal (out of control point) on a control chart.
2. The chance of the measurement system detecting a large shift.
3. The ability of the measurement system to track process improvements.

These three insights give you a very good understanding of the relative usefulness of the measurement system. The four classes of monitors are the best guidelines available to you for understanding how “good” your measurement system is. These four classes of monitors are compared to the AIAG acceptance criteria in this publication.

In this issue:

• MSA Review
• Gage R&R Example
• MSA Nomenclature
• The Problem is Not in the Calculations
• The Acceptance Criteria Problem Begins
• The Numbers Should Add to 100
• The Acceptance Criteria Issue for the ANOVA Method
• EMP Method: Four Classes of Monitors
• Comparing the AIAG Guidelines to the Classes of Monitors
• Summary
• Quick Links

You may download a pdf version of this publication at this link. Please feel free to leave a comment at the end of the newsletter.

MSA Review

This publication assumes you are familiar with MSA. If you are not, there are 23 previous publications on our website that explain the techniques in detail. These publications cover the three methods included below as well as nested MSA for non-destructive methods, the impact of probable error on specifications and control charts, etc. You can access these publications at this link.

The Average and Range Method as well as the ANOVA method are also covered in AIAG’s Measurement System Analysis, 4th Edition manual. The EMP method is presented in Dr. Wheeler’s book EMP III Evaluating the Measurement System Process. Dr. Wheeler’s book is highly recommended (www.spcpress.com).

Gage R&R Example

Of course, you need an example to do the comparisons between the four classes of monitors and the AIAG acceptance criteria. Suppose the thickness of a certain part is important to a major customer. You want to know how “good” the micrometer you use is, i.e., is the measurement system acceptable? You decide to run a Gage R&R by having 3 operators measure 5 parts 2 times each. You perform the Gage R&R using operators A, B and C. The data from the study are given in Table 1 below.

Table 1: Gage R&R Data

MSA Nomenclature

Before analyzing the results, let’s briefly discuss nomenclature. The AIAG and Dr. Wheeler use different nomenclatures. The nomenclature is shown in Table 2.

Table 2: MSA Nomenclature

This publication will focus on the value of GRR. The MSA methodologies give you insights into other things, but the value of GRR is the measure that is focused on by most people. The desire is to be able to compare GRR to the total variation to determine the % of the total variation that is due to the measurement system, i.e., the combined repeatability and reproducibility.

The Problem is Not in the Calculations

These results were analyzed using three different Gage R&R analysis techniques: Average and Range method, ANOVA method, and the EMP method. The results for all three methodologies give very similar results for the variables listed in Table 2. The SPC for Excel software was used to generate the results for the three different MSA methodologies. The standard deviations obtained by each methodology are summarized in Table 3.

Table 3: Standard Deviation Estimates for Gage R&R Methodologies

There are some minor differences in the results since the methodologies are different. However, the results are very similar for the three methodologies. It is not the calculations that is the issue – but the way the calculations are used to judge if the measurement system is acceptable. This is where AIAG runs into trouble with how it sets up its criteria.

The Acceptance Criteria Problem Begins

The problem with AIAG began when it began to use ratios to help define what is acceptable for a measurement system. Output from the Average and Range method will usually have values (in addition to the standard deviations above) that are expressed as a % of the Total Variation. These are ratios of each standard deviation to the total standard deviation (TV). This calculation is intended to represent the percentage of the total variation that is consumed by each standard deviation. For example, for EV:

% EV = EV/TV = 6.901/24.333 = 28.36%

This is interpreted as 28.36% of the total variation is consumed by the repeatability or equipment variation. The other calculations are shown below for the other standard deviations from the Average and Range method in Table 3.

%AV = AV/TV = 3.693/24.333 = 15.18%

%GRR = R&R/TV = 7.827/24.333 = 32.17%

%PV = PV/TV = 23.040/24.333 = 94.69%

The %GRR value is then compared to the AIAG guidelines for what makes a measurement system acceptable. These guidelines are:

• Under 10%: generally considered to be an adequate measurement system
• 10 % to 30%: may be acceptable for some applications
• Over 30%: considered to be unacceptable

The %GRR for this example is 32.17%. So, this measurement system is considered to be unacceptable. It says on page 78 of AIAG’s Measurement Systems Analysis, 4th Edition that “every effort should be made to improve the measurement system” when it is unacceptable.

There does not appear to be any rationale in using the values of 10% and 30% as the criteria. These have not changed over the years. In fact, the Average and Range method often compares the results to the specifications instead of the total variation – and use the same criteria when comparing the results to the specifications.

There is also a caution statement on that page: “the use of the GRR guidelines as threshold criteria alone is NOT an acceptable practice for determining the acceptability of a measurement system.”

How true. This is not the way to judge how acceptable a measurement system is – not even close. And it should never be used. Let’s explore why.

The Numbers Should Add to 100

I learned early in math that percentages of a total should add to 100. For example, if 4 out of 10 of us liked a movie and 6 did not, I would say that 40% liked the movie and 60% did not like it. And 40% + 60% = 100%.

That is not the case with the % of total variation numbers given above. GRR is the combined repeatability (EV) and reproducibility (AV).

%GRR = %EV + %AV = 28.36 + 15.18 = 43.54

But the %GRR listed above is 32.17%. Also, one would expect the % total variation to be the sum of the %EV, %AV and %PV. And I would expect it to be 100% since those three percentages make up everything! But,

%TV = %EV + %AV + %PV = 28.36 + 15.18 + 94.69 = 138.23

That is a little above 100%. What is happening?

Dr. Wheeler does a superb job of showing why these don’t add up to 100. He shows the trigonometric functions that give rise to the percentage values above. The percentages listed above are not proportions. But the fact that they are listed as percentages gives the impression that they are. The major reason is that standard deviations are not additive.

TV ≠ R&R + PV

Or in Dr. Wheeler’s nomenclature:

σ_x≠ σ_p+σ_e

The % of total variation used by AIAG treats the ratios as being proportions when they are not. It is the variances that are additive, not the standard deviations. It is the old Pythagorean Theorem we learned in our first geometry class. If you want to use proportions to talk about how much of the total variation is consumed by something, you must use variances – not the standard deviations. A variance is simply the square of the standard deviation. This changes the results considerably:

EV²/TV²=σ_pe²/σ_x²= 6.9012/24.3332 = 8.04%

AV²/TV²=σ_o²/σ_x²= 3.6932/24.3332 = 2.30%

GRR²/TV²=σ_e²/σ_x²= 7.8272/24.3332 = 10.35%

PV²/TV²=σ_p²/σ_x²= 23.0402/24.3332 = 89.65%

Now these percentages make sense. The repeatability and reproducibility add up to the Gage R&R. And the total adds to 100%. These ratios do tell us what % of the total variance is due to each source. Note that this is % of total variance, not total variation, which is based on the standard deviations. Table 4 compares the percentages based on using the standard deviation and the variances.

Table 4: Comparing the Standard Deviation Ratios and Variance Ratios

The Acceptance Criteria Issue for the ANOVA Method

The ANOVA method, like the EMP method, focuses on the variances, not the standard deviations. Both methods use the % of total variance, not the % of total variation in the Average and Range Method. So, what makes an acceptable measurement system under the ANOVA method? Unfortunately, it appears that the acceptable criteria are just the squares of the acceptance criteria given above for the Average and Range method. An acceptable measurement system under the Average and Range method is less than 10%. This is based on the standard deviations. Since the variance is simply the square of the standard deviation, an acceptable measurement system under the ANOVA method is 10% x 10% = 1%. Table 5 shows the acceptance criteria for the two methods.

Table 5: Acceptance Criteria for the Average and Range Method and the ANOVA Method

Using the standard deviations in Table 2, the ANOVA method has a %GRR:

σ_e²/σ_X²= 6.9082/23.7782 = 8.44%

This is almost to the unacceptable value of 9%.. Using the numbers from the Average and Range method, it is over 10% so it is unacceptable by that methodology.

Again, there does not appear to be any justification that I have found for these guidelines. Why 10% and 30% or 1% and 9%? But there is another method which uses rational thinking to determine how acceptable a measurement system is. And this is Dr. Wheeler’s EMP methodology and the four classes of monitors.

EMP Method: Classes of Monitors

As mentioned above, Dr. Wheeler divides a measurement system into four categories – First Class monitors, Second Class monitors, Third Class monitors and Fourth Class monitors based on how much the measurement system reduces the strength of a signal, the chance of the measurement system detecting a large shift in the data, and the ability of the measurement system to track process improvements. These three insights give you a very good understanding of the relative usefulness of the measurement system.

The basic equation describing the relationship between the total variance, the product variance and the measurement system variance is given below.

σ_x²= σ_p²+σ_e²

Dr. Wheeler uses the Intraclass Correlation Coefficient to define the class of monitor. The Intraclass Correlation Coefficient is simply the ratio of the product variance to the total variance and is denoted by ρ:

ρ= σ_p²/σ_x²

This is simply the % of the total variance that is due to product variance. Remembering the basic equation above, then 1 – ρ is the % of the total variance that is due to the measurement system (i.e., combined repeatability and reproducibility):

1 – ρ = 1 – σ_p²/σ_x²= (σ_x²– σ_p²)/σ_x²= σ_e²/σ_x²

So, 1 – ρ is the %GRR (compared to the total variance) that we calculated above. The value of ρ from the Average and Range method is

ρ = PV²/TV²= σ_p²/σ_x²= 23.0402/24.3332 = 0.8965

The Intraclass Correlation Coefficient is used to place the measurement system into one of four classes. Table 6 summarizes these classes and the characteristics of those classes.

Table 6: The Four Classes of Process Monitors

The first column lists the value of the Intraclass Correlation Coefficient. The second column lists whether it is a First Class, Second Class, Third Class or Fourth Class monitor – with “First” being the best. In the example above,ρ = 0.8965, so the measurement system is classified as a “First Class” monitor. But this is the same data that the AIAG guidelines said represented a measurement system that is unacceptable!

Remember that the % of the variance due to the measurement system is 1 –ρ.So, as you move from a First Class to a Fourth Class monitor the % of variance due to the measurement system is increasing.

The third column shows how much of a reduction in a process signal there is. The First Class monitor has less than a 10% reduction in process signal while a Fourth Class monitor has more than a 55% reduction in process signal. The fourth column lists the chance of detecting a ± 3 standard error shift within ten subgroups. This column refers to four rules. These are the four Western Electric zone tests:

• Rule 1: a point is beyond the lower or upper control limit
• Rule 2: two out of three consecutive points on the same side of the average are more than two standard deviations away from the average
• Rule 3: four out of five consecutive points on the same side of the average are more than one standard deviation away from the average
• Rule 4: Eight consecutive points are above or below the average

Note that the First and Second Class monitors detect Rule 1 very well. Once you reach a Third Class monitor, you need to apply all four rules to get the chance of detecting the shift high. Fourth Class monitors are not good at detecting any shifts essentially.

The fifth column describes the monitor’s ability to track process improvements. This is something we don’t think about too much. Suppose you make a great process improvement. Your Six Sigma team worked hard and reduced the variation in the process considerably – resulting in a significant improvement in your process capability value. What happened to your measurement system? Assuming you did not improve it, the % variance due to the measurement system increased as you made other improvements. This last column describes how much process improvement you can have until the measurement system moves from one class to another.

For more details on the four classes of monitors, please see this link.

Comparing the AIAG Guidelines to the Classes of Monitors

You can compare the AIAG guidelines to the classes of monitors by making use of the following:

1 – ρ= σ_e²/σ_x²

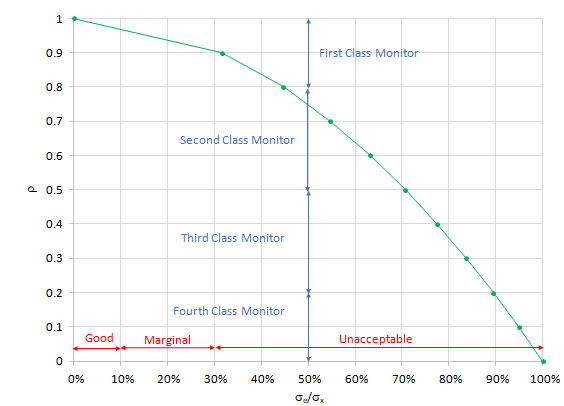
Table 7 shows the values of ρ versus σ_e/σ_x. Figure 1 is a plot of the data in Table 7.

Table 7: Comparing to the % GRR Based on Total Variation

Figure 1: ρ versus σ_e/σ_x

The First Class Monitor has ρ values between 0.8 and 1.0. This corresponds to a %GRR from 0 to 45%. This means that a measurement system responsible for up to 45% of the total variation can still be a First Class Monitor. Why is that? Because it has very little reduction in a signal from a control chart, it can pick up large shifts and it can be used to track process improvements. A Second Class Monitor can be responsible for up to 71% of the total variation. A Third Class Monitor can be responsible for up to 89% of the total variation.

It is clear that the AIAG approach overstates the impact of the measurement system on the results. Plus, the guidelines from AIAG are not based on the reality of what the measurement system is used for. The classes of monitors approach from Dr. Wheeler are based on what happens in reality.

Summary

This publication has compared the different approaches to MSA acceptance criteria. One approach is the AIAG methodology and acceptance criteria for the Average and Range method as well as the ANOVA method. The acceptance criteria do not accurately reflect the impact the measurement system has on the production process. In fact, there does not appear to be any relationship to the criteria and what actually occurs. The AIAG criteria overstate the impact that the measurement system has.

The Classes of Monitors approach has a basis in reality – what really happens in the process. It focuses rating a measurement system in the following three areas:

• How the measurement system can reduce the strength of a signal (out of control point) on a control chart.
• The chance of the measurement system detecting a large shift.
• The ability of the measurement system to track process improvements.

Based on these results, the measurement system can be classified as a First, Second, Third or Fourth Class Monitor.

The Average and Range Method, the ANOVA method, and the EMP method will give comparable results for the GRR as a percentage of total variance (not variation). But the only effective way to interpret the results is to use the Classes of Monitors approach. Do not use the AIAG acceptance criteria.