March 2017
(Note: all the previous SPC Knowledge Base in the basic statistics category are listed on the right-hand side. Select this link for information on the SPC for Excel software.)
Alpha and p-value. Two commonly used terms in statistical analysis. We hear these two terms quite often. Both are used in hypothesis testing where we are trying accept or reject a given hypothesis. We use them to help us decide if a regression model is “good” or if the predictor variables are “significant.” We use them to help us conclude if data comes from a specific distribution. Or we use them to decide if two processes operate at the same average or the same variation. Or we use them to determine what variables in an experimental design have an impact on the response variable. The list goes on and on. But what do these two terms really mean? This month’s publication looks at alpha and the p-value. One we choose. The other we calculate.
In this issue:
- Taking Data – There is Always Variation and Uncertainty
- Example
- Alpha
- p-Value
- Using Alpha and the p-value Together
- Summary
- Quick Links
You may download a pdf version of this publication at this link. Please fee free to leave a comment at the end of the publication.
Taking Data – There is Always Variation and Uncertainty
You run into alpha and the p-value when you take data from a process or processes, analyze that data, and try to draw a conclusion about the process or processes from which you took the data. For example, suppose you want to know if a quality characteristic (X) in a process has an average of 100. You take 20 observations from the process and measure the quality characteristic. You take the average of those 20 observations. This sample average is an estimate of the “true” but unknown process average for X (the quality characteristic). Is the sample average the same as the true average of X? Maybe yes but probably not.
If we repeat the process with 20 new observations, will the second sample average be the same as the first one? Again, maybe yes, but probably not. Why? Because there is always variation present, we don’t always get the same result each time.
There is variation and uncertainty in the results we get. We are trying to use these results to make a decision about our process. But because of this uncertainty, we have chance of making the wrong decision sometimes. The two terms, alpha and the p-value, help us deal with this uncertainty.
Example
In this publication, we will be exploring a known population. This population consists of 5000 data points randomly generated from a normal distribution. The data used are available for download at this link.
The average of these 5000 data points is 100.077. This is the true average of the population; it is the population average because we used all the possible outcomes in the population to calculate it. We will denote this population average by μ.
Now, suppose we don’t know the true average, but we want to know if it could be 100.077. We set up our null hypothesis (H0) and alternative hypothesis (H1) as follows:
H0: μ= 100.077
H1: μ≠ 100.077
For a more detail explanation, please see our publication on hypothesis testing. We take 20 random observations from our population. We want to use those 20 observations to estimate the population average. The results for the 20 observations are given in Table 1.
Table 1: Process Results
| 111.17 | 96.01 |
| 93.67 | 118.09 |
| 90.62 | 111.21 |
| 96.66 | 93.21 |
| 114.85 | 84.5 |
| 92.43 | 117.56 |
| 97.45 | 97.7 |
| 92.62 | 103.36 |
| 94.16 | 114.46 |
| 100.69 | 106.52 |
The sample average of these 20 observations is 101.3. This is our estimate of μ, the population average. Since there is variation in our results, the best we can do is to construct a confidence interval around our sample average and see if the value of 100.077 lies in that confidence interval. If it does, we will conclude that the population average is 100.077. If the interval does not contain 100.077, we will conclude that the population average is not equal to 100.077.
The confidence interval depends on three things: the significance level (alpha or α), the sample size (n), and the standard deviation (s). We select two of these: alpha and the sample size n.
Let’s talk about the significance level for a moment. The significance level is the probability of rejecting the null hypothesis when the null hypothesis is in fact true. Put simply, it is the probability that you make the wrong decision. Using statistics does not keep us from making wrong decisions. The most typical value of the significance (our alpha) level is 0.05. We will use 0.05 in this example. Since alpha is a probability, it must be between 0 and 1. In this example, we are willing to make a mistake 5% of the time. Note that you pick the value of alpha.
The equation for the confidence interval around a mean is given below.
where zα/2 is the standard normal distribution z score with a tail area of α/2. We will use the normal distribution in this example.
The 20 observations were analyzed using SPC for Excel software. Part of the results are shown in Table 2. The mean of the 20 observations is 101.3. This is the value we are going to compare to our hypothesized mean of 100.077.
Table 2: Results
| Mean | 101.3 |
| Standard Deviation (s) | 10.09 |
| Sample Size | 20 |
| Standard Error of Mean | 2.255 |
| Degrees of Freedom | 19 |
| Alpha | 0.05 |
| z (0.025) | 1.960 |
| Lower Confidence Limit | 96.93 |
| Upper Confidence Limit | 105.77 |
| Hypothesized Mean | 100.077 |
| z | 0.563 |
| p-Value | 0.5734 |
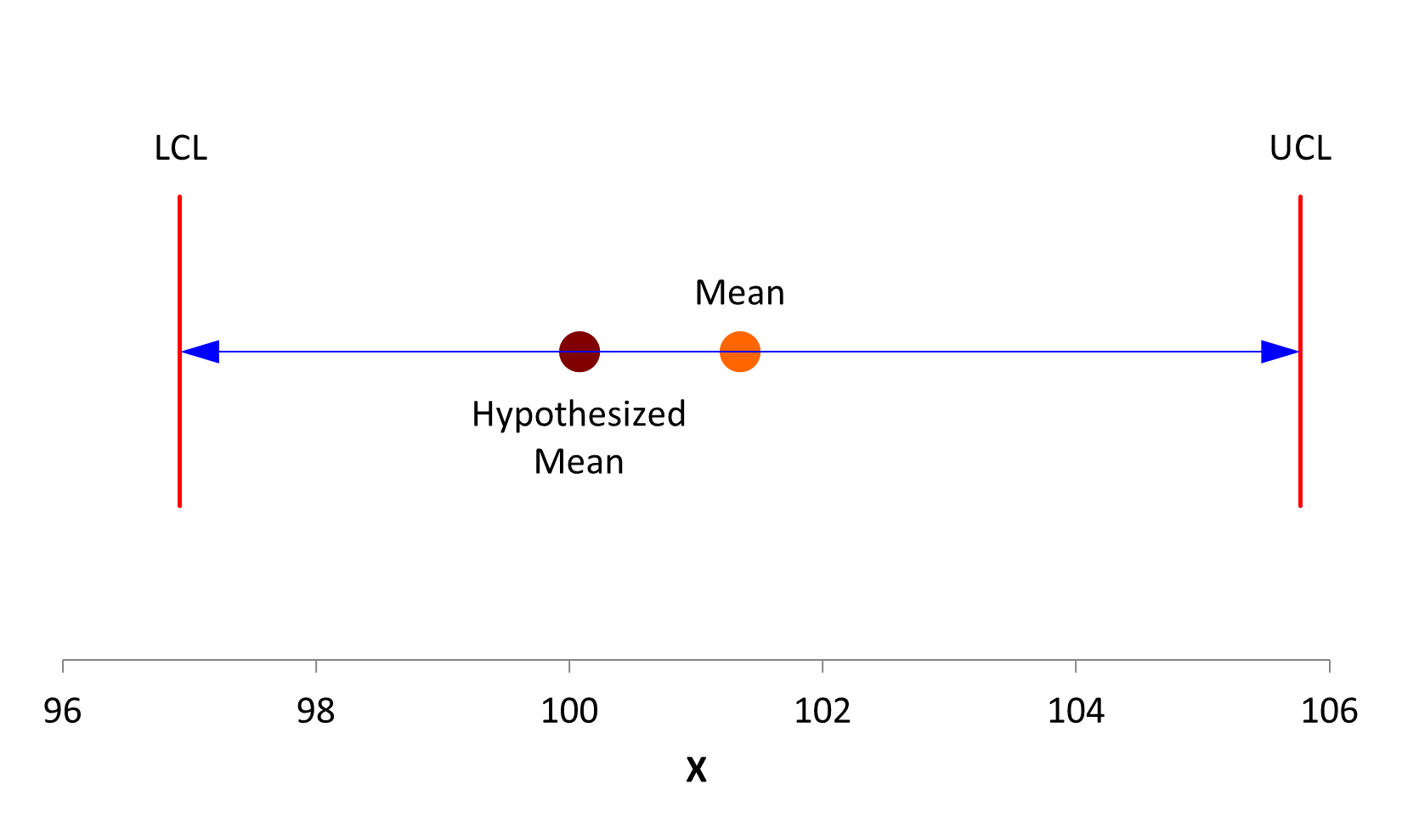
The table contains the confidence interval. The lower confidence limit is 96.93. The upper confidence limit is 105.77. This interval contains our hypothesized mean of 100.077. So, based on this sample, we conclude that the null hypothesis is true and our population is 100.077. This is shown graphically in Figure 1 (also part of the SPC for Excel output).
Figure 1: Confidence Limit
The table includes the value of alpha we picked (0.05) as well as the value of z used in the above equation, which is based on alpha. We also see a p-value of 0.5734. Let’s take a closer look at alpha.
Alpha
We mentioned that alpha was the probability of rejecting the null hypothesis when it was in fact true. Its value is often 5%. This means, that if we repeat the above process of taking 20 observations and constructing a confidence interval each time, 5 times out of 100, the confidence interval will not contain the true average of 100.077. And we would make the wrong decision – reject that the true average is 100.077 when in fact it is true.
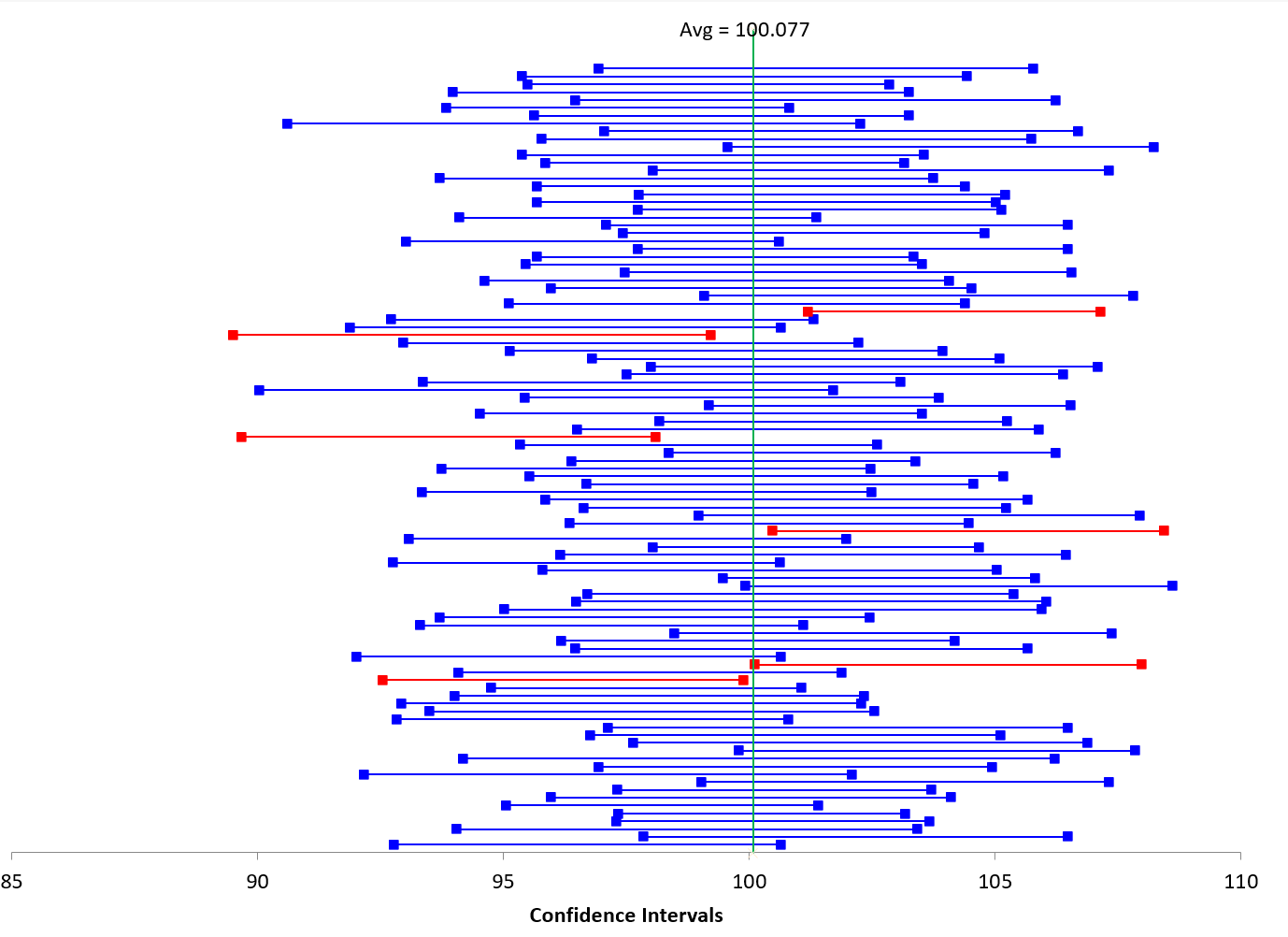
The process was repeated 100 times for the population we are using. Twenty observations were selected at random and the confidence interval constructed. Of those 100 confidence intervals, 6 did not contain the true average of 100.077. This is shown in Figure 2. The red confidence limits do not contain the true average and, in those 6 instances, we would make the wrong decision.
Figure 2: 100 Confidence Intervals
Remember, you pick the value of alpha. You decide what risk you are willing to accept. Is 5% an appropriate risk for every situation? No, not all. Maybe you’re dealing with something related to safety. Is 5% adequate in safety? No, you probably want 1% or something even less. In other situations, you might be willing to live with 10% error. The key is that you make the decision – you decide on the value of alpha.
p-Value
While we pick the value of alpha, the p-value is a calculated value. It is calculated different ways depending on the statistical technique but the interpretation is the same. The p-value can be interpreted as the probability of getting a result that is as extreme or more extreme when the null hypothesis is true. The p-value in the results in Table 2 is 0.5734. The sample mean is 101.3. The absolute deviation from the average is |101.3 – 100.077| = 1.223. This means that there is a 57.34% probability of getting a sample mean result that is greater than +/- 1.223 from the average. Since this probability is large, we conclude that the null hypothesis is true.
What if the p-value was small, like 0.03? In this case, there is only a 3% chance of obtaining this sample result or something more extreme. We would reject the null hypothesis.
Another way of looking at the p-value is to examine the z value for the sample average. Remember that a z value measures how far, in standard deviations, a value is from the average. The z value for a sample average is given below.
So, the sample average of 101.3 is 0.563 standard deviations from the hypothesized mean. The probability of getting |z| is the p-value of 0.5734.
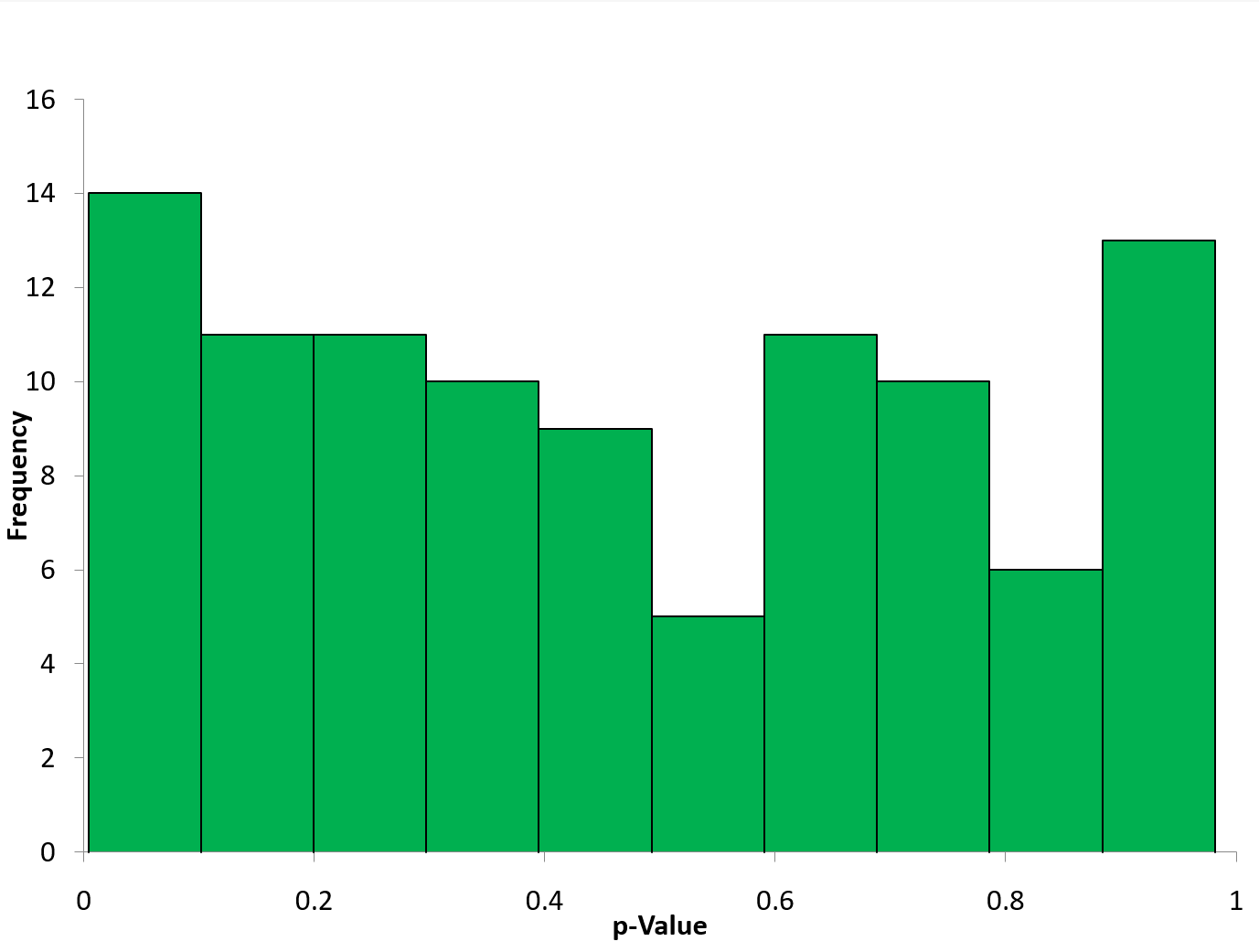
How does the p-value vary with random samples over time? It turns out it varies much more than you would think. The p-values were calculated for each those 100 random samples with 20 observations shown in Figure 2. The maximum p-value was 0.982. The minimum p-value was 0.004. That is a large range when taking 20 random observations from the same population. The distribution of the p-values is shown in Figure 3.
Figure 3: Distribution the p-value for 100 Random Samples
The chart almost looks like a uniform distribution. In this case, it is. With continuous data and assuming the null hypothesis is true, the p-values are distributed uniformly between 0 and 1.
Remember, a p-value measures the probability of getting a result that is at least extreme as the one we have – assuming the null hypothesis is true. It does not measure the probability that the hypothesis is true. It is wrong to say that if the p-value is 10%, there is a 10% probability that the hypothesis is true. Nor does it measure the probability of rejecting the null hypothesis when it is true. That is what alpha does.
Using Alpha and the p-value Together
So, how do we use these two terms together. Basically, you decide on a value for alpha. What probability of being wrong do you want to use? What makes you comfortable? Suppose that is alpha = 0.10. You then collect the data and calculate the p-value. If the p-value is greater than alpha, you assume that the null hypothesis is true. If the p-value is less than alpha, you assume that null hypothesis is false. What do you do if the two values are very close? For example, maybe the p-value is 0.06 and alpha is 0.05. It is your call to make in those cases. You can always choose to collect more data.
Note that the confidence interval and p-value will always go to the same conclusion. If the p-value is less than alpha, then the confidence interval will not contain the hypothesized mean. If the p-value is greater than alpha, the confidence interval will contain the hypothesized mean.
Summary
This publication examined how to interpret alpha and the p-value. Alpha, the significance level, is the probability that you will make the mistake of rejecting the null hypothesis when in fact it is true. The p-value measures the probability of getting a more extreme value than the one you got from the experiment. If the p-value is greater than alpha, you accept the null hypothesis. If it is less than alpha, you reject the null hypothesis.
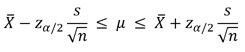
When you wrote "This means that there is a 57.34% probability of obtaining a mean of 101.3 or larger if the null hypothesis is true" you were overlooking the low tail of the distribution. The probability of a mean of 101.35 or larger is only 28.67% if the null hypothesis is true, so the probability of that large an absolute deviation from the null hypothesis can be 57.34%.
You are correct as usual. I should have applied it to the upper portion of the distibution only once you know what the sample aveage is. I revised the wording to reflect your comments.
Wow, thanks for your super clear explanation!
"If the p-value is greater than alpha, you accept the null hypothesis."Oh no, accepting the null hypothesis is a big 'ol no-no. Just because your sample isn't extreme enough for you to reject the null hypothesis doesn't mean that there isn't another sample that exists that /is/ extreme enough for you to reject the null.To avoid making a Type II error, we would usually say that we "fail to reject the H0" or "do not reject the H0.""The p-value measures the probability of getting a more extreme value than the one you got from the experiment."Close! You said it better earlier in the page, but it is still best to say "The p-value measures the probability of getting a more extreme value than the one you got from the experiment (assuming the null is true)." I'm sure you were trying to keep things short, but stating the assumption is still important.
Is the a better way to conclude when the P value is less than or equal to the alpha in a meaningful way to the average educator like a teacher?
Not sure what you mean, but I think Figure 1 makes it clear if there is a significant difference or not – good visual picture.
This was a well written and thorough explanation of both concepts. Thank you so much!!
“What do you do if the two values are very close? For example, maybe the p-value is 0.06 and alpha is 0.05. It is your call to make in those cases. You can always choose to collect more data.”This is an absolute abuse of the experiment, called p-hacking, because after you continue collecting data and get *new* p-value, you have to use all knowledge about both p-values you got when you decide to reject / not reject H0. To make life easier, run only one experiment with enough sample size determined by pre-chosen statistical power and make only one conclusion. You cannot fully explain the nature of statistical tests without mentioning probabilty of type 2 error “beta”, which tells about statistical power.
Collecting more of the same data is not p-hacking i don't believe. My understanding of p-hacking is that you perform many statistical tests on the data and only report those that come back with significant results. This is one statistical dataset that you are adding more data to.
I agree that you should set the alpha and beta values before you run your experiemnt. But in real life, you can't sometimes take all those samples.
https://www.spcforexcel.com/knowledge/basic-statistics/how-many-samples-do-i-need
I believe you used the word "accept the null hypothesis" when instead you should have said "retain the null hypothesis". It's a small thing, but you can't "accept" a null hypothesis.I knew what you were trying to say though (I was just chewed out for making the same mistake in my sociology course).
I have not heard it quite like that using retained. I think he makes a big deal out of nothing. I usually frame it like:
The null hypothesis is accepted. There is no evidence that the difference in means is not equal to 0.
or
The null hypothesis is rejected. There is evidence that the difference in means is not equal to 0.
well not really, in every statistic course I took, especially the entry-level ones, we were taught not to use "accept the null", you either "reject" or "fail to reject", but you never "accept"
thank you for your thorough answer
Thank you!