October 2013
Have you ever had to support your position that your measurement system is well suited for its intended purpose? This addition to our SPC knowledge database takes a look at how you can do this when a part is altered or destroyed during testing. Our SPC knowledge database has additional articles on how to perform other types of Gage R&R studies.
Any Gage R&R study is really an experiment to determine the various sources of variation. How you set up the experiment determines what sources of variation you can analyze. Last month we took a look at the differences in how a classical Gage R&R study and a destructive Gage R&R study are set up. In the classical Gage R&R study, a part is not altered or destroyed – you can re-test the same part multiple times. With a destructive Gage R&R study, the part is destroyed or altered during testing and you cannot measure it multiple times. This month’s addition to our SPC knowledge base examines how you analyze a destructive Gage R&R study.
In this issue:
- Destructive Gage R&R Analysis Setup
- Example Data
- Results of Destructive Gage R&R
- ANOVA Table
- Contribution to Total Variance
- Contribution to Total Standard Deviation, Specifications and Process Standard Deviation
- Summary
- Quick Links
Destructive Gage R&R Analysis Setup
We will start with a quick review of how a destructive Gage R&R experiment is set up. Since the part or sample is altered or destroyed during testing, it cannot be retested. For example, in heat treating of steel tubes, a tensile test is often done to measure tensile strength. The sample is destroyed during testing so you cannot have the same or different operators test that sample again.
Without the ability to retest, how can you estimate the Gage R&R? There are two critical items here. First, you have to be able to assume that a batch of material is so close to the same that you can reasonably assume that the parts in the batch are the “same” part. This means that the batch is homogeneous. In the perfect world, if you took any sample from that batch, the test result would be the same. Second is the design setup. If all the operators can measure parts from each batch, then you can use the traditional method of running a Gage R&R – the crossed design. However, if each operator cannot measure parts from each batch (e.g., not enough parts from each batch to do this), then a nested Gage R&R must be used.
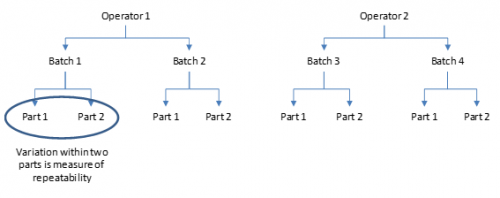
Figure 1 shows how a destructive Gage R&R is laid out. In this example, there are only two parts from each batch. This is not enough for every operator to run parts from each batch since the part is destroyed during testing. Operator 1 runs two parts from batch 1 and two parts from batch 2. Operator 2 runs two parts from batch 3 and two parts from batch 4. The batches are different. Since each batch is unique to a single operator, this is called a nested Gage R&R.
Figure 1: Destructive (Nested) Gage R&R
Example Data
You are involved in heat treating of parts and want to perform a Gage R&R analysis on the hardness tester. To measure hardness, a piece of the product is cut, prepared and tested. That piece is altered, so it cannot be retested. The parts are produced in small batches. You are confident that the parts within a batch are homogeneous. You want to include three operators in the Gage R&R study. You would like each operator to test two parts per batch. But there are not always enough parts for each operator to test parts from each batch. You will have to use a nested design. You decide to use 15 batches and take 2 parts from each batch. Operator 1 will measure the two parts for batches 1 to 5; operator 2 will measure 2 parts from batches 6 -10; and operator 3 will measure 2 parts from batches 11 – 15. The resulting from the Gage R&R study are shown in Table 1.
Table 1: Nested Gage R&R Raw Data
| Operator | Batch | Result | Operator | Batch | Result | |
| A | 1 | 33.4 | B | 8 | 34.7 | |
| A | 1 | 33.2 | B | 9 | 32.4 | |
| A | 2 | 32.4 | B | 9 | 33.1 | |
| A | 2 | 31.7 | B | 10 | 34.8 | |
| A | 3 | 34.4 | B | 10 | 34.9 | |
| A | 3 | 34.5 | C | 11 | 32.6 | |
| A | 4 | 33.9 | C | 11 | 32.7 | |
| A | 4 | 34.5 | C | 12 | 32.3 | |
| A | 5 | 34.5 | C | 12 | 32.1 | |
| A | 5 | 34.7 | C | 13 | 34.9 | |
| B | 6 | 32.5 | C | 13 | 34.7 | |
| B | 6 | 32.1 | C | 14 | 33 | |
| B | 7 | 32.1 | C | 14 | 33.2 | |
| B | 7 | 32.3 | C | 15 | 31.6 | |
| B | 8 | 35.1 | C | 15 | 30.9 |
Results of Destructive Gage R&R
We will use analysis of variance (ANOVA) to analyze the results of our destructive Gage R&R study. This analysis method was described in detail on our three part series on ANOVA Gage R&R. You can review these newsletters for more information on the calculations. We will show the results here.
The data were analyzed using the SPC for Excel software package. Remember there are three things you can compare the Gage R&R results to:
- Total variation in the parts in the study
- Process standard deviation
- Specifications
Which of these you use depends on how you use the measurement system. If you are using the measurement for process control or SPC, then you use the first or second method above. If you are using the measurement system for inspection only, you would use the specification approach. We will see the results for all three here.
To use the process standard deviation, you need an estimate of that standard deviation. It can come from a control chart kept in production or from calculating the standard deviation from a large amount of production data (be wary of special causes). Suppose you have done that and your process standard deviation is 2.5. The specifications for hardness are 30 to 38.
ANOVA Table
The ANOVA table for these data is shown in Table 2.
Table 2: ANOVA for Hardness Nested Gage R&R
| Source | df | SS | MS | F | p Value |
| Operator | 2 | 4.363 | 2.181 | 0.696 | 0.5176 |
| Batch | 12 | 37.606 | 3.134 | 38.849 | 0.0000 |
| Repeatability | 15 | 1.210 | 0.081 | ||
| Total | 29 | 43.179 |
The first column is the source of variability. Remember that a Gage R&R study is a study of variation. There are four sources of variability in this ANOVA approach: the operator, the batch, the repeatability, and the total. Note that the batches are nested within operators. This is sometimes denoted as “Batch (Operator).”
The second column is the degrees of freedom associated with the source of variation. The degrees of freedom integer is simply the number of values of a statistic that are free to vary. For example, suppose you have a sample that contains n observations. We use the sample to estimate something – usually an average. When we want to estimate something, it costs us one degree of freedom. So, if we have n observations and want to estimate the average, then we have n – 1 degrees of freedom left.
The third column is the sum of squares (SS) associated with the source of variation. The sum of squares is a measure of variation. It measures the squared deviations around an average.
The fourth column is the mean square associated with the source of variation. The mean square is the estimate of the variance for that source of variability based on the amount of data we have (the degrees of freedom). So, the mean square is the sum of squares divided by the degrees of freedom. The mean square is the value that we will use to estimate different variances.
The fifth column is the F value. This is the statistic that is calculated to determine if the source of variability is statistically significant. It is the ratio of two variances (or mean squares in this case). The sixth column contains the p value. The p column is the column we want to examine first. If the p value is less than 0.05, it means that the source of variation has a significant impact on the results. In this example, the “batch” has significant impact on the results, while “operator” does not. This is what you want – it means that the measurement system can distinguish between the parts used in the study. Gage R&R studies attempt to quantify this by determine the % Gage R&R value.
Contribution to Total Variance
The best way to examine results is by looking at each source’s contribution to the total variance. This approach uses the variation of the parts uses in the study. Table 3 shows the results for this example.
Table 3: Contribution to Total Variance
| Source | Variance Component |
% Contribution |
| Repeatability | 0.0807 | 5.02% |
| Reproducibility | 0.000 | 0.00% |
| Total Gage R&R | 0.0807 | 5.02% |
| Part-to-Part | 1.527 | 94.98% |
| Total Variation | 1.607 | 100.00% |
The first column is the source of variation. The second column is the variance component for that source. Note that the variance for the repeatability is the same as the mean square for repeatability in the ANOVA table. The other mean squares in the ANOVA are used to estimate the variances for the part-to-part variation and total variation.
The last column in Table 3 is the % contribution to the total variation. This column is determined by dividing the source’s variance by the total variance. For example:
% contribution due to Total Gage R&R = 0.0807/1.607 = 5.02%
A rule of thumb often used to determine if a measurement system is acceptable is as follows:
- % Gage R&R ≤ 10%: measurement systems is acceptable
- 10% < % Gage R&R < 30%: measurement system may or may not be acceptable depending on its use and the customer
- %Gage R&R ≥ 30%: measurement system needs improvement
Note that the variance component column is additive, i.e., the total variation is sum of the individual sources of variation.
So, based on these results, the hardness tester is responsible for about 5% of the total variance. This test method appears to be very good.
Contribution to Total Standard Deviation, Specifications and Process Standard Deviation
There are three other ways to look at the results. You can look at the contribution each source has to the total standard deviation from the study, to the specifications, and the process standard deviation. These results are shown in Table 4.
Table 4: Other Contributions
| Source | Stand. Dev. | 6*SD | % Contribution | % Tolerance | % Process |
| Repeatability | 0.284 | 1.704 | 22.40% | 21.30% | 11.36% |
| Reproducibility | 0.000 | 0.000 | 0.00% | 0.00% | 0.00% |
| Total Gage R&R | 0.284 | 1.704 | 22.40% | 21.30% | 11.36% |
| Part-to-Part | 1.236 | 7.413 | 97.46% | 92.67% | 49.42% |
| Total Variation | 1.268 | 7.607 | 100.00% | 95.08% | 50.71% |
Again, the first column is the source of variation. The second column in the standard deviation. This is simply the square root of the variances given in Table 3. Note that this column is not additive – the total standard deviation does not equal the sum of the standard deviation of the individual sources. This is why the last two columns in the table do not sum to 100%.
The column “6*SD” is six times the standard deviation of the source of variation. This is the “spread” that is used to “judge” the standard deviation against. It is based on the fact that most of the data for a normal distribution is within +/- 3 standard deviations of the averages – or is contained in a spread of 6 standard deviations.
The “% Contribution” column is determined by dividing the 6*SD spread for the source of variation by the value of 6*SD for the total variation. Thus for total Gage R&R:
% contribution for total Gage R&R = 1.704/7.607 = 22.4%
This means that the “spread” of the Gage R&R takes up 22.4% of the total spread. Note that the % total Gage R&R % contribution is 22.4% – compared to 5.02% when looking at the variances. This result implies that the test method may need some work.
You can also compare the standard deviation to the specification range. The % tolerance column does this and is the 6*SD spread for the source of variation divided by the tolerance range (38 – 30) = 8. For example,
% of total tolerance due to Gage R&R = 1.704/8 = 21.3%.
This means that the Gage R&R spread takes up 21.3 % of the tolerance spread.
The column labelled “% Process” is determined by dividing the 6*SD for the individual source of variation by the process spread, which is 6 times the process standard deviation. In this example, we estimated that the process standard deviation was 2.5. So,
% of total process spread due to Gage R&R = 1.704/(6*2.5) = 11.36%
This means that the Gage R&R spread takes up about 11% of the total process spread.
Summary
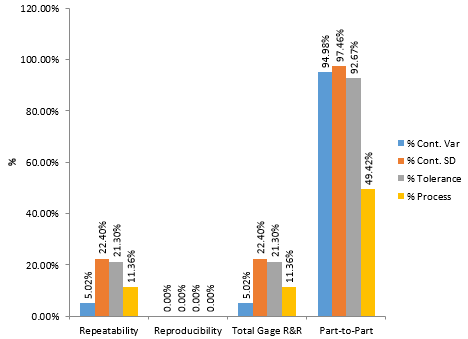
The chart in Figure 1 summarizes the results. You can see that the results vary depending on what you are comparing the results against – the variation in the parts (using either the variance of standard deviation approach), the tolerance, or a known process standard deviation.
Figure 1: Variance Components for Destructive Gage R&R
This is one reason that Gage R&R is not crystal clear at times. The results depend on how you analyze the results. But in the end, whether or not a measurement system is acceptable depends on you and your customer.
This month’s addition to our SPC knowledge base has looked at how you analyze a destructive (nested) Gage R&R experiment. In this type of experiment, the part is destroyed or altered and cannot be re-measured.
Wonderful! I like it! Please carry on similar study and please share the same time to time.it will help all of our practitioners to get their further improving their body of the knowledge.
With regards,
K.M.mostafa Anwar
Lean Six Sigma Green Belt
Good I like itPlease share simlar studies With RegaardsPVK RajuSix sigma Black belt
If are considering the parts within the batch are identical in that case why we were not able to calculate reproducibility?
You do calculate reproducibility. It is just very small in this example. If there were larger differences between the "same" sample results, it would show up. Bill
Hi!!I tried to calculate the reproducibility standard deviation and its coming out to be 0.473 which makes the % Contribution to Total Variation = 16.22% and GRR % Contribution to Total Variation = 22.07%.Please correct it else let me know if I am wrong.RegardsAshok
The formula for reproducibility is (MS Operator – MS(Batch/Operator))/(parts*samples)
MS Operator = 2.18 while MS Batch = 3.134
so MS Operator – MS Batch is negative – so it rounds up to zero.
This is great! It helped me a lot. Keep it up!
Hi,Can you provide wiith the formulas used to calculate all the ANOVA tables? I am unable to solve the problem.or attach a excel sheet that you may have put togther for solving this as a template to understand it better.Thank youDee
The basic calculations are covered in our three part series on ANOVA Gage R&R. Please take a look at those and see if that helps you solve the problem. If not, I will put the formulas here.
Bill, Thanks for your writeup. We are performing compressive strength testing. Due to the natural of our products, there are variations from the same batch. We just completed a GRR study using 15 batchs of samples, 4 specimens per batch, 2 operators. Gage R&R is 80%. However, the total COV (SD/Mean) of all specimens is less than 2%. the COV of the specimens is about 2-3% range. This cov is considered to be great for strenght testing such as compression and tensile strength. There are 2 possible conclusions among my colleagues: 1. our measurement is not good enough. 2. Gage R&R is not suitable for this application because it assumes the the 4 specimens in the same batch are identical.I would appreciate if you could shine some lights on this.Thanks,
Hello,
Can you send me the data so I can run an analysis (<a href="mailto:bill@www.spcforexcel.com">bill@www.spcforexcel.com</a>). Both possible conclusions are possible. But I can see more by running the analysis to see the various source of variability.
Thanks.
Hi, you mentioned in the example about Nested Gage R&R that the tolerance is 8 but when I check the data depend on this formula UCL-LCL Ifoud the Tolerance is 6.4968 when UCL=X bar bar+3 sigma and LCL=x bar bar-3 sigma?
The tolerance is the width of the specification limit. In this case, USL – LSL = 38 – 30 = 8.
Is it the tolerance or range? RANGE/WIDTH = UCL-LCL
I am not sure what you are asking. The width of the tolerance is USL – LSL. You can also call it a range.
Hi,how we can compute the residuals for the data above because it is Nested design and is there any software can do that or your SPC pakage can do that because I need to analyze the data if it is has outlier or not through Residuals .I have similar dataThanks
A Gage R&R study is really a designed experiment – whether it is nested or not. You are looking for signals from the data. You search for outliers by doing a range control chart on the "same" runs. As long as there are no out of control points on the range control chart, you assume there are no outliers.
The most gage RR article/studies I've come across assume that there is only one operator involved. What if there are 2 group of operators in the process or for that matter two distinct measurement tools also. This is something that I need to test; we have one set of operators who pull a sample from a batch and another set of operators who run the sample on an equipment and there happens to be two pieces of equipment that they can run the sample on (same equipment but different generations). If there are 3 operators that pull the sample, and 3 operators that run the sample on any/both of these two equipment and we take 3 batches with 2 samples each (destructive) then it is 108 readings. But is this resolution good enough against the complexity or should we simplify by breaking the process into 2 groups or something similar. I think the equipment could be looked at as two separate studies. Thanks!
GAge R&R is a study in variation. Repeatability is the ability of a single operator to measure the same value on the test, while reproducibility is the ability of multiple operators to measure the same value on the test. So one operator studies only give you the repeatability. You should look at each measurement system individually.
Logically, it seems that one should only use a Nested design here IF one believes that parts from a given Batch are IDENTICAL when tested by the same Operator, but will be DIFFERENT when tested by different Operators. (A Minitab blog makes this point directly in explaining the purpose of the Nested Gage R&R for destructive testing.)In most cases, attributing such adaptive behavoir to parts would be difficult to defend, so one should use the simpler Crossed design analysis, and accept that test Repeatability will be confounded wih part-to-part variation. Here that gives the same low Repeatability of 0.284 (ANOVA, or 0.296 by SPC), but now Operator Reproducibility and Operator*Batch interaction (non-parallelism) become inconveniently large and significant. After all, something must explain why the variation among the six samples from any Batch tends to be so much larger than the variation among two samples from the same Batch by any given Operator. (It's not likely to just be bad luck in Part-to-Part variation than only shows up across different Operators!)My guess is that labs may use the Nested Gage R&R more than they should because they don't like to fess up to Operator irreproducibility, and would rather blame it on Part-to-Part variation typically outside their control.
Thanks for the comment. It is uncommon for the batch-to-batch variation to be large compared to the witihn-batch variation. I grew up in the PVC industry and that was very true. So, if you did a control chart with subgrouping based on within-batch variation, the control limits were very tight and everything was out of control. Hence, the need for the Xbar-mR-R chart. Cross designs are great if you have the same part or sample to test for each operator. But with destructive testing, you don't have the same part/sample. Thus, the need for the nested design. I know the logic of saying the parts from the same batch are the "same" and then you can use a crossed design. But what is the operational defintion of the "same" or "identifical"? I have seen variation in the hardness along a length of steel bar that was very large. Cutting the bar into parts and calling them same is definitely questionable. In the end, it is the choice of the person running the test. He/she has to use his/her knowledge of the process and make that call. But if you believe the parts are the "same," I would agree with your comments.
Bill
Bill, thanks for your quick response, but I think you missed my point, so I'll try again.A nested model would apply if a given Operator (magically?) could test the same part twice, while different Operators could never test the same part. That is what nesting by Operator implies. My point is that is rarely the case with destructive testing, where each part usually can only be tested/broken once. More typically, the logical Gage R&R for destructive testing truly would be an equal opportunity crossed design, with measurement repeatability hopelessly confounded with part-to-part variation for all Operators — unless there is information not in evidence to separate them outside of the core R&R design itself.Applying the logic of nesting to your example data set for a destructive test, without providing a reason to believe that a given Operator can replicate a test on essentially the same part while different Operators can't, seems totally wrong to me. Taken at face value, your data set suggests major Reproducibility issues between Operators, while the combination of Part-to-Part variation and pure measurement error is relatively small (sterr=0.28 with dof=15).Minitab's "A Simple Guide to Gage R&R for Destructive Testing" (Paret, 2013) engaged in special pleading to argue that situational constraints would sometimes (certainly not always) naturally approximate a nested situation (even though the experimenter might prefer the more powerful crossed design). I don't think your example and interpretation make sense without proposing a similar special case. Nested R&Rs are not a general approach for destructive testing, nor will Crossed R&Rs give as much information as we'd like (unless part-to-part variation is relatively minor compared to batch-to-batch variation). Analysis as Nested R&R while simply using representative parts from each batch as you seem to suggest would result in disguising any Operator Reproducibility issues under Part-to-Part variation.
Thank you for the extremely thoughtful response, DaveW. Thank you also, Bill, for the very helpful articles.I am in a situation where my test is destructive. While it is difficult, we can get enough parts reasonably considered to be "the same" to perform repetitions across multiple operators. Understanding where error will be moved depending on my experimental layout is important to me, because I want to make improvements to my system, not disguise a problem. You have both been a great help in this effort. Thank you.
Hi Steve,
Please see this writeup as well: https://www.spcforexcel.com/knowledge/measurement-systems-analysis/gage-rr-for-non-destructive-and-destructive-test-methods
Best Regards,
Bill
what is the relation ship between GR&R and CoV study
The coefficent of variation is the ratio of the standard deviation to the mean. I am not sure what you are asking.
bill,% of total tolerance results are different from minitab
Why do you think the % total tolerance is different from Minitab? The specs are 30 to 38. The numbers in the newsletter match Minitab results.
Hi bill thanx for such useful information. I hv a question on process capability cpk. Why we take cpk min. In thr results of cpu &cpl.
That gives you the mimimum capability value. If you just see Cpk, you don't know if it is Cpl or Cpu – you just know the minimum of the two If Cpk = 1.33 then you know the spec limit that is closest to the average if 4 standard deviations away and essentially nothing is out of spec at all.
Hi Bill,Thanks a lot for this nice example. A minor observation if I am not mistaken. The Gage R&R acceptance criteria you are referring to are valid for the Gage R&R standard deviation (%) and not for the Gage R&R variance (%).% Gage R&R ≤ 10%: measurement systems is acceptable;10% < % Gage R&R < 30%: measurement system may or may not be acceptable depending on its use and the customer%Gage R&R ≥ 30%: measurement system needs improvement So these rules for the Gage R&R variance (%) are:% Gage R&R ≤ 1%; measurement systems is acceptable;1% < % Gage R&R < 9%; measurement system may or may not be acceptable;% Gage R&R ≥ 9%: measurement system needs improvement.In your example, the Gage R&R variance (%) is 5.02%, the system may or may not be acceptable. Taking the square root of 5.02% gives us 22.8% with the same conclusion.
Thanks for the comment. Yes, you are correct. Please see this link:
https://www.spcforexcel.com/knowledge/measurement-systems-analysis/acceptance-criteria-for-MSA
Hola, por favor asesoramiento para llevar a cabo un sistema de medicion no replicable para una camara salina.Saludos
Not sure i understand what you want. Is there no way to divide a sample in half and test both havles?
Hi, thanks for sharing the knowledge here. Can you please tell more about the Resolution in MSA. When do we need to lood at Resolutioin, how to calculate, and is there's a spec/standard for judging it? Thanks.
You are welcome. Probable error defines the resolution of the meaurement system. Please see this link:
https://www.spcforexcel.com/knowledge/measurement-systems-analysis/probable-error-and-your-measurement-system
Thanks
Hi, May I know what is the formula for degree of freedom in Batch and Repeatibility?I referred to previous 3 series but seems like there is some differences.Thank you.
Let o = number of operators, df = o – 1 = 3 -1 = 2
Let b = number of batches per operator: df = o(b-1) = 3(5 – 1) = 12
Let r = number of replications: df = ob(r – 1) = 3*5*(2-1) = 15
Total df = obr-1 = 3*5*2 – 1 = 29
Remember that this is a nested gage R&R; the equations will be different for a crossed Gage R&R.
Hi.. What will be the degree of freedom for reproducibility?
Reproducibility is a measure of the difference between operators. Since this is a nested design, the impact of operators are spread over two things: Operators and Batch(Operators).
Batch
12
37.606
In Table 2 how the value 37.606 arrived
Hi Bill,Thanks for your detailed explanation. I would like to ask for guideline of part/batch. In your example, 2 parts each are drawn from 15 batches. Can I draw 10 parts each from 3 batches(assuming my processa is stable)? In short, do we prefer more parts from less batches or less parts from more batches?
Thanks. Yes you can use 10 parts from 3 batches. The key is to get enough data. you want around 30 degrees of freedom total.
Hello Bill,
Thank you. I was struggling to design a study for tensile strength measurment when I found thisvery detailed post. I have a question about the way SSbatch was obtained. As you said last year when answering Khor message, the equations are different in nested and crossed gage R&R. Could you give us the formula? Thanks Cerdic