February 2015

You can analyze the Gage R&R study using one of the following analysis techniques:
- Average and Range Method
- ANOVA
- EMP (Evaluating the Measurement Process)
All three techniques have been covered in detail in past publications. This publication compares the output from the three techniques and attempts to decide which is best. We will assume that we want to use the test method for process control.
In this issue:
- The Data
- The Sources of Variation in a Gage R&R Study
- Average and Range Gage R&R Analysis
- ANOVA Gage R&R Analysis
- EMP Gage R&R Analysis
- Comparison of Results
- Summary
- Quick Links
You may download a pdf copy of this publication here.
The Data
The data we will use is from the 4th edition of the Measurement Systems Analysis manual published by AIAG. In this Gage R&R study, there are three operators and ten parts. Each operator runs each part three times. The data are shown in Table 1.
For example, operator A ran part 1 three times with the following results: 0.29, 0.41, and 0.64. The data from this table are analyzed using each of the three Gage R&R analysis techniques using the SPC for Excel software. Before we start, we will quickly review the sources of variation in a Gage R&R study. There are four sources we primarily follow: repeatability, reproducibility, part, and total.
Table 1: The Data
| Op. | Trial/Part | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 1 | 0.29 | -0.56 | 1.34 | 0.47 | -0.8 | 0.02 | 0.59 | -0.31 | 2.26 | -1.36 |
| A | 2 | 0.41 | -0.68 | 1.17 | 0.5 | -0.92 | -0.11 | 0.75 | -0.2 | 1.99 | -1.25 |
| A | 3 | 0.64 | -0.58 | 1.27 | 0.64 | -0.84 | -0.21 | 0.66 | -0.17 | 2.01 | -1.31 |
| B | 1 | 0.08 | -0.47 | 1.19 | 0.01 | -0.56 | -0.2 | 0.47 | -0.63 | 1.8 | -1.68 |
| B | 2 | 0.25 | -1.22 | 0.94 | 1.03 | -1.2 | 0.22 | 0.55 | 0.08 | 2.12 | -1.62 |
| B | 3 | 0.07 | -0.68 | 1.34 | 0.2 | -1.28 | 0.06 | 0.83 | -0.34 | 2.19 | -1.5 |
| C | 1 | 0.04 | -1.38 | 0.88 | 0.14 | -1.46 | -0.29 | 0.02 | -0.46 | 1.77 | -1.49 |
| C | 2 | -0.11 | -1.13 | 1.09 | 0.2 | -1.07 | -0.67 | 0.01 | -0.56 | 1.45 | -1.77 |
| C | 3 | -0.15 | -0.96 | 0.67 | 0.11 | -1.45 | -0.49 | 0.21 | -0.49 | 1.87 | -2.16 |
The Sources of Variation in a Gage R&R Study

- Repeatability is the variation in the measurements obtained by one operator measuring the same item repeatedly. This is also called measurement or equipment variation.
- Reproducibility is the variation of the measurement system caused by differences in the way operators perform the test. It is the variation in the average values obtained by several operators while measuring the same item and is sometimes called the appraiser variation.
The combined repeatability and reproducibility make up the Gage R&R variability. The third major source of variation is the part variation. This variation is a measure of how much the parts vary and should be representative of what occurs in production if you are using the measurement system to control the process. The last major source of variation is the total variation – which is a measure of the variation in all the results.
The relationship between the total, part and measurement system variation is given by the equation below
where the subscripts represent the source (t = total, p = part, and ms = measurement system). Note that this equality is based on variances. Remember that the variance is the square of the standard deviation (sigma).
Average and Range Gage R&R Analysis

The average and range method forms subgroups based on each operator-part combination (e.g., one subgroup is A-1 for operator A and part 1). The three trials from Table 1 make up that subgroup (0.29, 0.41, 0.64). Subgroup averages and ranges are calculated. Each operator’s average and range is then calculated. The average range for the three operators is then found. In this example, the average range is R = 0.342. To find the repeatability (called EV = equipment variation by AIAG), this average range is multiplied by a constant, K1, that depends on the number of trials. For 3 trials, K1 = 0.5908. Thus,
EV = R (K1) = (0.342)(0.5908) =0.202
A word of caution here. The value of EV does not represent a variance. It represents a standard deviation. This is the start of the problems associated with the average and range method.
The range in operator averages is then calculated. This is called XDIFF and is 0.445 in this example. This value is used in the following equation to find the reproducibility or the appraiser variability (AV).
where K2 is a constant that depends on the number of operators (0.5231 for three operators), n is the number of parts (10) and r is the number of trials (3). The value of AV for our example dada is 0.230
The Gage R&R value is then found by combining the EV and AV results using the following equation:
The part variation (PV) is found by determining the range in part values (Rp) and multiplying this range by a constant (K3) that depends on the number of parts. For this example:
PV = Rp(K3) = (3.511)(0.3146) = 1.105
Finally, the total variation (TV) is then found by the following equation:
Again, not that the above equation for TV is not the variance – but the variation represented by the standard deviation. We can use these results to determine the % of variation (NOT variance) due to each source of variation. The results are shown in Table 2.
Table 2: Average and Range Method Gage R&R Results
| Measurement Unit Analysis | % Total Variation (TV) |
|---|---|
| Repeatability – Equipment Variation (EV) | |
| EV =0.202 | %EV=EV/TV = 17.61% |
| Reproducibility – Operator Variation (AV) | |
| AV = 0.230 | %AV =AV/TV = 20.04% |
| Repeatability & Reproducibility (R & R) | |
| R&R = 0.306 | % R&R =R&R/TV=26.68% |
| Part Variation (PV) | |
| PV=1.104 | PV =PV/TV=96.37% |
| Total Variation (TV) | |
| TV =1.146 |

So, what does this value of %R&R mean? The acceptance criteria from AIAG are given on page 78 of their measurement system analysis manual. The criteria given there are reproduced in Table 3 below.
Table 3: AIAG Gage R&R Acceptance Criteria*
| % R&R | Decision | Comments |
|---|---|---|
| Under 10 | Generally considered to be an acceptable measurements system. | Recommended, especially useful when trying to sort or classify parts or when tightened process control is required. |
| 10 to 30 | May be acceptable for some applications. | Decision should be based upon for example, importance of the application measurement, cost of measurement device, cost of rework or repair. Should be approved the customer. |
| Over 30 | Considered to be unacceptable | Every effort should be made to improve the measurement system. |
* from Measurement Systems Analysis, 4th Edition, 2010, AIAG
The manual does say that these criteria alone are not an acceptable practice for determining the acceptability of a test method. They are just guidelines. But, in reality, many people do just that. So, with our value of 26.88% for the % R&R, we would conclude that the test method may or may not be acceptable – it depends on the situation.
ANOVA Gage R&R Analysis
Analysis of variance (ANOVA) is a technique that examines what sources of variation have a significant impact on the results. This approach actually adds another source of variation to the mix: the operator*part interaction. This interaction is usually not significant so we will leave it out of this discussion. What ANOVA does is compare the variation in part and operator results to the repeatability of the test method.
The Gage R&R output for our example is shown below. Remember, there is no operator*part interaction so it was taken out of the ANOVA table below.
Table 4: ANOVA Gage R&R without Interaction Report
| Source | df | SS | MS | F | p Value |
|---|---|---|---|---|---|
| Part | 9 | 88.362 | 9.818 | 245.614 | 0 |
| Operator | 2 | 3.167 | 1.584 | 39.617 | 0 |
| Repeatability | 78 | 3.118 | 0.04 | ||
| Total | 89 | 94.647 |
The fourth column is the mean square associated with the source of variation. The mean square is the estimate of the variance for that source of variability (not necessarily by itself) based on the amount of data we have (the degrees of freedom). So, the mean square is the sum of squares divided by the degrees of freedom. We use the mean square information to estimate the variance of each source of variation – this is the key to analyzing the Gage R&R results.
The fifth column is the F value. This is the statistic that is calculated to determine if the source of variability is statistically significant. It is based on the ratio of two variances (or mean squares in this case). The last column is the p value – a value ≤ 0.05 is considered significant. So, both the parts and operator have a significant effect on the results.
With ANOVA, you determine the % of the total variance (not standard deviation) due to each source. The following equations can be used to calculate the variances when there is no operator*part interaction. The repeatability variance is simply the mean square of the repeatability source of variation.
The reproducibility comes from the mean square of the operators (with n = number of trials and p = number of parts):
The part variance comes from the mean square of the parts (where o = number of operators).
The results are shown in Table 5. The calculations are covered in our September 2012 publication.
Table 5: % Contribution to Variance by Source
| Source | Variance | % Contr. |
|---|---|---|
| Total Gage R&R | 0.0914 | 7.76% |
| Repeatability | 0.0400 | 3.39% |
| Reproducibility | 0.0515 | 4.37% |
| Part-to-Part | 1.086 | 92.24% |
| Total Variation | 1.178 | 100.00% |
From this analysis, the % Gage R&R is 7.76%. The AIAG reference manual does include ANOVA as a way of analyzing a Gage R&R study. In fact, using these same data, the manual now says that the test method is acceptable since the % Gage R&R is below 10. What? How can it be one thing with the Average and Range method and another with the ANOVA? You probably already know the answer, but we will review it later. Next, we look at the EMP methodology.
EMP Gage R&R Analysis

The approach, not surprisingly since it is Dr. Donald Wheeler’s approach, includes the use of control charts. A range chart is made based on the subgroups composed of each operator-part combination. As long as the range chart is in statistical control, the repeatability can be estimated from the average range (using Dr. Wheeler’s nomenclature):
where d2 is a control chart constant that depends on subgroup size (the number of trials). The numerical results of the calculations are shown in the table below.
The range of operator averages is used to find the reproducibility using the following:
where R0 is the range of the operator averages,d2* is a bias correction factor that depends on the number of operators, n = number of trials, o = number of operators, and p = number of parts.
The combined R&R variance is the sum of the repeatability variance and the reproducibility variance:
The range of the p part averages is used to determine the product variance using the following:
The total variance is the sum of the product variance and the combined Gage R&R variance:
The variances for each source of variation are shown in Table 6. The last column is the % of total variance due to each source of variation.
Table 6: Contribution to % Variance using EMP Methodology
| Component | Variance | % of Total |
|---|---|---|
| Repeatability | 0.0407 | 3.1% |
| Reproducibility | 0.0531 | 4.1% |
| R&R | 0.0938 | 7.2% |
| Product | 1.216 | 92.8% |
| Total | 1.310 |
These results are very close to those obtained from the ANOVA Gage R&R methodology. Now, lets compare the results.
Comparison of Results
The results are compared in Table 7. The source is given in the first column. The average and range method results are given first. There has been an addition to the results for the Average and Range method. The first two columns under the Average and Range results are based on the calculations shown above – which use the standard deviation for the results. Those standard deviations were squared to generate variances and then the % of Total Variance was calculated for the Average and Range method.
Table 7: Comparison of Results
| Average and Range | ANOVA | EMP | ||||||
| Source | Variation | % of Total Variation | Variance | % of Total Variance | Variance | % of Total Variance | Variance | % of Total Variance |
| Repeatability | 0.202 | 17.61% | 0.04 | 3.11% | 0.04 | 3.39% | 0.0407 | 3.10% |
| Reproducibility | 0.23 | 20.04% | 0.05 | 4.03% | 0.0515 | 4.37% | 0.0531 | 4.10% |
| R&R | 0.306 | 26.68% | 0.09 | 7.13% | 0.0914 | 7.76% | 0.0938 | 7.20% |
| Product | 1.104 | 96.37% | 1.22 | 92.80% | 1.086 | 92.24% | 1.216 | 92.80% |
| Total | 1.146 | 1.31 | 100.00% | 1.178 | 100.00% | 1.31 | 100.00% | |
Note that the columns for variance and % of total variance are very close for all three methods. So, the three methods, when using the variance, generate very similar results.

So, the % of variation column does not sum to 100. This makes it much more difficult to interpret the results. Why AIAG continues to include the Average and Range approach in their manual is beyond me. At a minimum, all they have to do is to square the results to convert the results to variances. Bottom line: If you must use the Average/Range method, do not pay attention to the % of variation information (based on standard deviation). Use the % of variance information. It is essentially the same with all three methods.
But the bigger question is how to interpret the results. The criteria given by AIAG are just guidelines to consider (see Table 3). But if you apply them directly to the variance, most of the % of variance range is unacceptable – anything over 30% is not acceptable.
Dr. Wheeler’s EMP approach uses a completely different method. He classifies the test method as a First, Second, Third or Fourth Class monitor based on the intraclass correlation coefficient (?), which is the ratio of the part variance to the total variance:
The subscripts are as follows: x = total variance, p = part variance, e = measurement system variance. So the intraclass correlation coefficient is also equal to 1 minus the % of variance due to the measurement system (the % R&R).
Table 8 shows how Dr. Wheeler suggests the results be interpreted. The last column in the table was added to show the %R&R value and AIAG guidelines for acceptability.
Table 8: Interpreting the EMP Results
| ? | Type of Monitor | Reduction of Process Signal | Chance of Detecting ± 3 Std. Error Shift | Ability to Track Process Improvements | % R&R/AIAG Guideline |
|---|---|---|---|---|---|
| 0.8 to 1.0 | First Class | Less than 10% | More than 99% with Rule 1 | Up to Cp80 | 0 to 20%/Acceptable to Marginal |
| 0.5 to 0.8 | Second Class | From 10% to 30% | More than 88% with Rule 1 | Up to Cp50 | 20 to 50%/Marginal to Unacceptable |
| 0.2 to 0.5 | Third Class | From 30% to 55% | More than 91% with Rules 1, 2, 3 and 4 | Up to Cp20 | 50% to 80%/Unacceptable |
| 0.0 to 0.2 | Fourth Class | More than 55% | Rapidly Vanishing | Unable to Track | 80% to 100%/Unacceptable |
Note: table adapted from EMP III Evaluating the Measurement System, by Donald J. Wheeler, 2006 SPC Press.
This table was described in detail in our previous publication. Please refer to that publication for more information. The first column lists the value of the Intraclass Correlation Coefficient. The second column lists whether it is a First Class, Second Class, Third Class or Fourth Class monitor – with “First” being the best. The rest of the table (except the last column I added) gives information about how much a reduction in process signal there is, the chance of detecting a major shift, and the ability to track process improvements.
You can see from the table, a First Class Monitor has a % R&R range of 0 to 20%. Under the AIAG guideline, a test method is acceptable if the % R&R is 10% of less. It is marginal in the range of 10 to 30%. The % R&R for our example data is about 7%. So, it is First Class Monitor and acceptable under AIAG guidelines. This means that there is less than a 10% reduction in a process signal, there is a better than 99% chance of detecting a point beyond the control limits (Rule 1) and that the measurement system will be able to track process improvements up to Cp80. Cp80 is calculated based on specifications and marks the point from the measurement system will move from a first class to a second class monitor. Rules 2 to 4 are the zone tests. Wow, a lot more information than the guidelines in Table 3.
But, if the result was 15% R&R, it would be marginal under AIAG guidelines but still be a First Class Monitor. It appears to me that the AIAG guidelines are unduly restrictive. A Third Class monitor would be unacceptable under the AIAG guidelines but from the table above still can be used to track a process.
So, what should you do to analyze a Gage R&R study? Use the ANOVA or EMP method to analyze the Gage R&R study. They will give similar results for % of variance. The EMP method does have some control charting built into it which gives it the edge to me (see our last month’s publication). Then interpret the results using Dr. Wheeler’s approach in Table 8. Rate the test method as a First, Second, Third or Fourth Class monitor and then use the information in the table to understand what that means.
Summary
In our early publications, I said that a precise measurement system was one where the measurement system was in statistical control and the % of variance due to the measurement system was less than 10% of the total variance. This would make it a Class One Monitor under Dr. Wheeler’s system. So, was I wrong? Well, I too was probably too restrictive. I do believe that critical test methods should be monitored on an ongoing basis by running a control and analyzing the results using an individuals control chart. The objective should also be continuous reduction in the measurement system variability.
But for Gage R&R studies, use the ANOVA or EMP methodology and interpret the results as a First, Second, Third or Fourth class monitor. Forget about the Average and Range method results based on the standard deviation and their guidelines for what makes an acceptable measurement system.
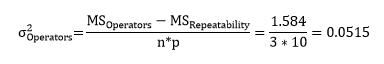

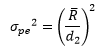
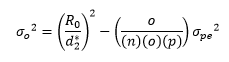
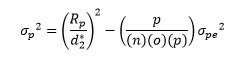
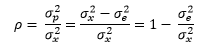
From reading Wheeler, my understanding is that the fault here lies with the AIAG (using % of total standard deviation) rather than anything about the Average & Range method of interpretation.Running your Gauge R&R example data in Minitab 17, I found that its two available methods (ANOVA and Average & Range) give practically indentical results, where for both the reported % of variance is useful and the reported % of standard deviation isn't (and adds up to well over 100% for both methods).
My question is about how to handle a measurement that is a vector. In my particular case, I am looking at an Unbalance reading of a rotor that has a magnitude and an angle. I am only looking at Static Balance. If I visualize the total tolerance zone of a certain magnitude, the tolerance zone would be a 360 degree tolerance zone of radius of what the maximum permissible deviation from the perfect part would be. Now, if I wanted to find the If I visualize the tolerance zone, I would see that it is basically a circle. I would say that the diameter of the circle would be basically the diameter of the circle as described by the range of say 30 measurements of the same part. Then, I would say that the P/Tol would be the area or the Repeatability/ Area of the total Tolerance Zone. Do you agree with my assessment. Is there a program developed for such a meaurement?
Hi Terrance,
I have not done anything with measurements that are a vector and how to handle process capability with that. I am sure that there are programs to handle it. Try searching for multiple process capability vectors.
Our manufacturing partner in Asia uses an Excel template for the Average and Range Method. However, their template does not compute the part variation, nor total variation. The % variation is done be dividing EV, AV, and R&R by the Tolerance (USL-LSL). Does anyone endorse this particular statistic?
It depends on what you are using the test for. If you are using it for control charting and process capability, you want to use the total variation because you want the test to be able to tell the difference between samples from the process. However, if you are just using the test to see if the product is in or out of spec, you use the tolerance range. Both are widely used depending on the purpose of the test method.
Dear Bill,Kindly share links or example where GRR has been done on two similar machines for destructive sampling. RegardsAshok
Hello Ashok,
I don't have any links on that. Maybe some readers do.
Does anyone have the table of the d2* constants ?
These are available in a number of books (like Dr. Wheeler's). You call also search online for d2* constants to find some results.
This is a very thorough article, easy to read and understand. I've been manipulating GRR template files without understanding the basics of it and found it confusing recently when I got different results using JMP software.This article helped me greatly understanding. Thank you so much!
What is the percentage of study variation and repeatability and also NDC target..
Please see this link: https://www.spcforexcel.com/knowledge/measurement-systems-analysis/acceptance-criteria-for-MSA
What is the origin of the table of the constant d2 the R&R stady ??
d2 is a bias correction factors; they come from "Tables of Range and Studentized Range" Annals of Mathematical Statistics, v.31, pp. 1122 – 1147, 1960 by H. L. Harter. You might check this article out: https://www.spcpress.com/pdf/DJW353.pdf
Bill, I am confused by one of your last paragraphs:” Under the AIAG guideline, a test method is acceptable if the % R&R is 10% of less. It is marginal in the range of 10 to 30%. The % R&R for our example data is about 7%. So, it is First Class Monitor and acceptable under AIAG guidelines. “But the AIAG guideline applies to R&R expressed as % of total variation (i.e., square root of variance). 30% as R&R/TV means 9% as R&R/Total variance. So that would be the threshold for AIAG-marginal. Can you please clarify?
Hello, if you use the AIAG guidelines based on varinace, you are correct. Acceptable is less than 1% of the total variance, marginal is 1 to 9% and not good is over 9%. Please see this article: https://www.spcforexcel.com/knowledge/measurement-systems-analysis/acceptance-criteria-for-MSA
if two measuring methods are used how to find who has better repeatability ? The higher value or lower value is considered?
The system with the lower measurement system standard deviation will be more repeatable.
Thanks for finally writing about >Three Methods to Analyze
Gage R&R Studies – SPC for Excel <Liked it!